Hello everyone,
When I was using the cvx toolbox to do a geometric programming optimization, the objective function is to maximize “t”, but I found some iterations it does not increase the objective function, it decreases it instead. Codes are attached below, please take a look, thank you.
Matrices a_kk, b_kk, c_k, and vector p can be treated as constants, q1 and t are two variables need to be solved.
The problem is not with Geometric Programming. The problem is with crude, unsafeguarded SCA.
Thank you for the answer. So is there anything I can do with it? The problem itself is a geometric programming, and it always has its convex form. Should I write a numerical algorithm by myself? Or if there is any other way to solve it? Thank you.
I looked more carefully at your program, and see that there is an unmatched end dangling at the end. Is that just an end of function which doesn’t do anything, or is there a missing while or for missing from your code images?
Is there actually a loop in which CVX is called more than once (more than once through cvx_begin ... cvx_end)? If so, it looks like each time through cvx_begin ... cvx_end would be solving the exact same problem instance. I
And in general, I am confused at to what you did and what results you obtained. What is q = q1 doing. It doesn’t appear that q is used for anything.
Please copy and paste the entire code, using Prefomatted text icon, rather than posting images. Please post all the solver and CVX output. And make sure the output you show is obtained from running the exact code you show.
Could you please explain what is Preformatted text icon?
Here is something about the code, you can see some new variables coming out, GAMMA_paper, Delta, D, R, rho, tau. These variables are been defined within the .mat file I loaded at the beginning.
To answer your question, I need to show you more details about my problem.
My problem is about maximizing the minimum Signal-to-Interference-and-Noise Ratio (SINR), that’s why I need t, t is an auxiliary variable indicates the lower bound of all SINRs.
My optimization including two subsections per iteration, one is to optimize vector u by using Rayleigh Quotient, and the other section is to optimize vector q. The ‘end’ you saw at the very end is related to the big ‘for’ loop which is used to adjust iteration times. And the ‘q = q1’ is just a simple replacement, because it seems that I can’t use the variable showing up previously within the cvx function again.
clc
clear all
load system_variable_setup.mat;
q_max = 0.5;
q = q_max*rand(1,50);
A = zeros(10,10,50);
B = zeros(10,10,50);
u = zeros(10,50);
c_max = 3;
for counter = 1:c_max
eigenval_max_cum = [];
for i = 1:50
A(:,:,i) = q(i)*GAMMA_paper(:,i)*GAMMA_paper(:,i).';
copilots_idx_logical = sum(user_pilots(i,:) == user_pilots,2) == tau;
copilots = find(copilots_idx_logical);
copilots(copilots == i) = [];
Delta_squared = zeros(10,10);
for j = 1:numel(copilots)
Delta_squared = q(copilots(j))*Delta(:,:,i,copilots(j))*Delta(:,:,i,copilots(j)).' + Delta_squared;
end
D_sum = zeros(10,10);
for k = 1:50
D_sum = q(k)*D(:,:,i,k) + D_sum;
end
B(:,:,i) = Delta_squared + D_sum + R(:,:,i)/rho;
L = chol(B(:,:,i));
A_trans = inv(L.')*A(:,:,i)*inv(L);
[eigenvec,eigenval] = eig(A_trans);
eigenval_max = max(max(diag(eigenval)));
[row,col] = find(eigenval == eigenval_max);
u(:,i) = inv(L)*eigenvec(:,col);
u(:,i) = u(:,i)/norm(u(:,i));
eigenval_max_cum = [eigenval_max_cum;eigenval_max];
end
% disp(u);
% disp(eigenval_max_cum);
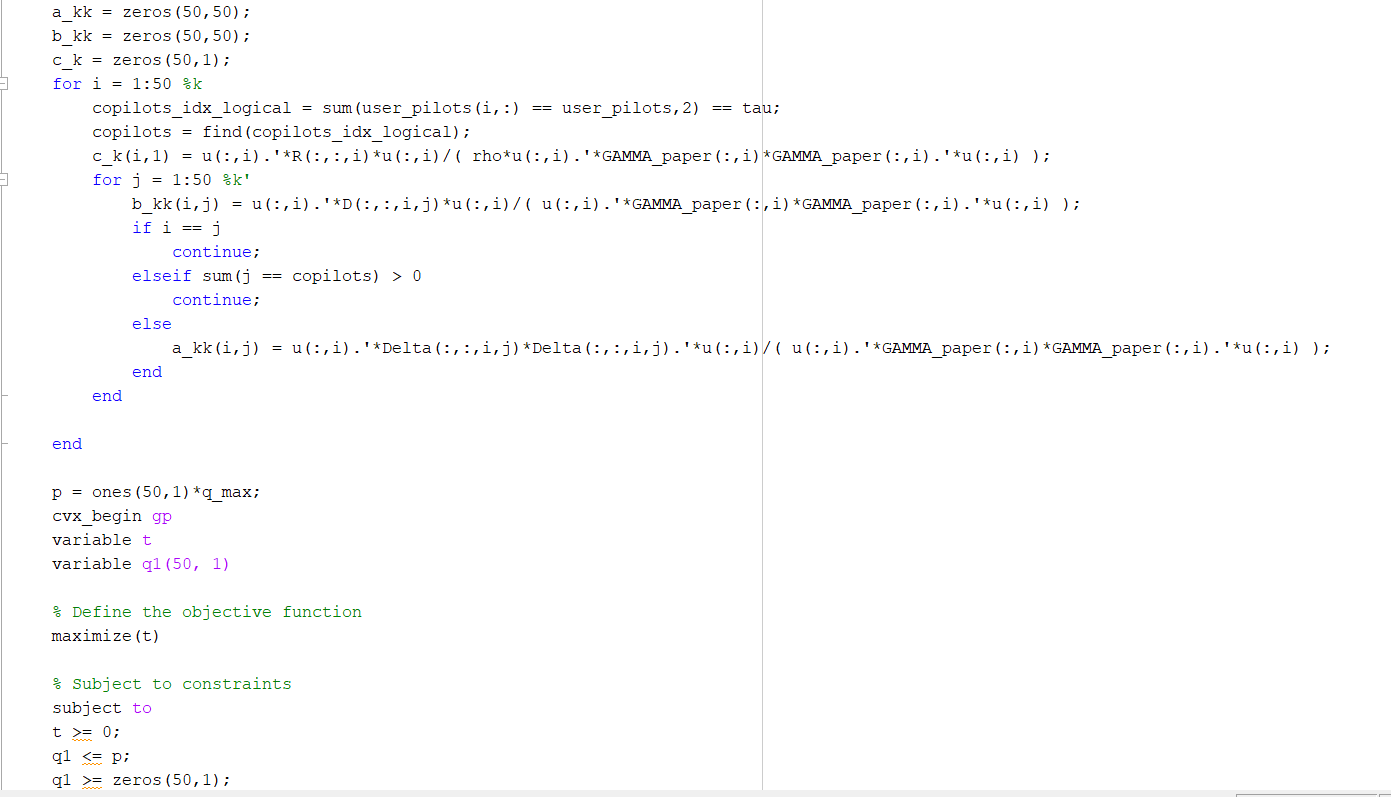
a_kk = zeros(50,50);
b_kk = zeros(50,50);
c_k = zeros(50,1);
for i = 1:50 %k
copilots_idx_logical = sum(user_pilots(i,:) == user_pilots,2) == tau;
copilots = find(copilots_idx_logical);
c_k(i,1) = u(:,i).'*R(:,:,i)*u(:,i)/( rho*u(:,i).'*GAMMA_paper(:,i)*GAMMA_paper(:,i).'*u(:,i) );
for j = 1:50 %k'
b_kk(i,j) = u(:,i).'*D(:,:,i,j)*u(:,i)/( u(:,i).'*GAMMA_paper(:,i)*GAMMA_paper(:,i).'*u(:,i) );
if i == j
continue;
elseif sum(j == copilots) > 0
continue;
else
a_kk(i,j) = u(:,i).'*Delta(:,:,i,j)*Delta(:,:,i,j).'*u(:,i)/( u(:,i).'*GAMMA_paper(:,i)*GAMMA_paper(:,i).'*u(:,i) );
end
end
end
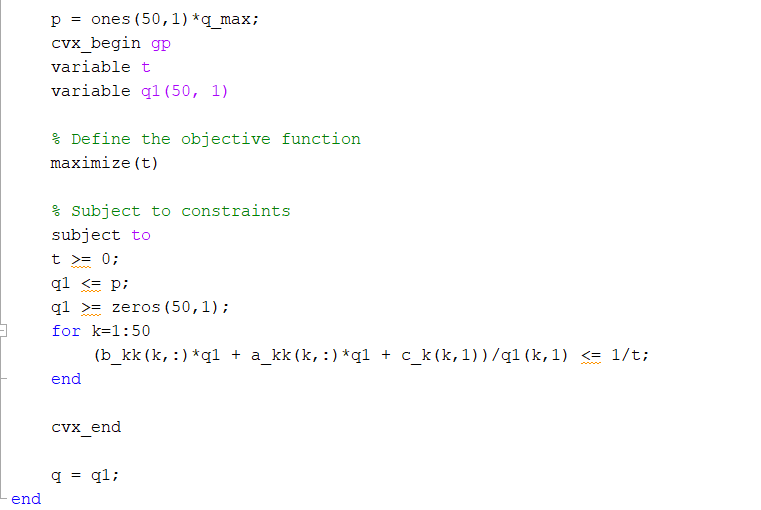
p = ones(50,1)*q_max;
cvx_begin gp
variable t
variable q1(50, 1)
% Define the objective function
maximize(t)
% Subject to constraints
subject to
t >= 0;
q1 <= p;
q1 >= zeros(50,1);
for k=1:50
(b_kk(k,:)*q1 + a_kk(k,:)*q1 + c_k(k,1))/q1(k,1) <= 1/t;
end
cvx_end
q = q1;
end
Here is the output
Successive approximation method to be employed.
For improved efficiency, SDPT3 is solving the dual problem.
SDPT3 will be called several times to refine the solution.
Original size: 7802 variables, 2651 equality constraints
2550 exponentials add 20400 variables, 12750 equality constraints
-----------------------------------------------------------------
Cones | Errors |
Mov/Act | Centering Exp cone Poly cone | Status
--------+---------------------------------+---------
2550/2550 | 8.000e+00 7.574e+00 0.000e+00 | Solved
2550/2550 | 4.658e+00 1.242e+00 1.954e-05 | Solved
2550/2550 | 3.905e-01 1.288e-02 0.000e+00 | Solved
2209/2216 | 8.536e-03 5.863e-06 0.000e+00 | Solved
0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Solved
-----------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +0.0249061
Successive approximation method to be employed.
For improved efficiency, SDPT3 is solving the dual problem.
SDPT3 will be called several times to refine the solution.
Original size: 7802 variables, 2651 equality constraints
2550 exponentials add 20400 variables, 12750 equality constraints
-----------------------------------------------------------------
Cones | Errors |
Mov/Act | Centering Exp cone Poly cone | Status
--------+---------------------------------+---------
2550/2550 | 8.000e+00 8.583e+00 0.000e+00 | Solved
2548/2548 | 6.242e+00 2.033e+00 0.000e+00 | Solved
2550/2550 | 3.989e-01 1.344e-02 2.295e-05 | Solved
2380/2424 | 8.976e-03 1.642e-05 1.525e-05 | Solved
0/ 28 | 2.757e-06 1.533e-05 1.528e-05 | Solved
-----------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +0.0245157
Successive approximation method to be employed.
For improved efficiency, SDPT3 is solving the dual problem.
SDPT3 will be called several times to refine the solution.
Original size: 7802 variables, 2651 equality constraints
2550 exponentials add 20400 variables, 12750 equality constraints
-----------------------------------------------------------------
Cones | Errors |
Mov/Act | Centering Exp cone Poly cone | Status
--------+---------------------------------+---------
2550/2550 | 8.000e+00 9.854e+00 0.000e+00 | Solved
2550/2550 | 7.959e+00s 3.022e+00 4.375e-04 | Solved
2550/2550 | 4.132e-01 1.446e-02 8.674e-04 | Solved
1987/2001 | 9.470e-03 7.216e-06 0.000e+00 | Solved
0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Solved
-----------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +0.0234127
Now that you showed the whole program, which is different than what you posted before, I see that you are calling CVX iteratively within SCA. Therefore, my first post applies, specifically, including everything in the link I provided.
Perhaps you should consider trying to use a non-convex solver under YALMIP.
If you do stay with CVX, I recommend you use Mosek as solver if available to you, otherwise install CVXQUAD with its ecponential.m replacement, as discussed in CVXQUAD: How to use CVXQUAD's Pade Approximant instead of CVX's unreliable Successive Approximation for GP mode, log, exp, entr, rel_entr, kl_div, log_det, det_rootn, exponential cone. CVXQUAD's Quantum (Matrix) Entropy & Matrix Log related functions
However, it does appear that CVX’s Successive Approximation method did solve your problem and that the difficulty in your case is that SCA is a lousy algorithm, which neither Mosek not CVXQUAD will fix for you.
The whole program and output are both just posted, please take a look. I saw you mentioned about non-convex solver in the link you posted. What confused me is that, my problem is a convex optimization, then why should I use the non-convex solver? I mean GP is not always convex, but it always has its convex form right?
Then should I use CVXQUAD and MOSEK or not, you mean neither of them will work well for my problem right?
I already edited my post when I saw your output.
Each time through cvx_begin gp ... cvx_end is a convex geometric Programming problem. The non-convexity arises because you are calling CVX iteratively, each time “comvexifying” your original problem by changing a variable to input data. That is what is non-robust.
If you usegp mode in CVX, it is best to use Mosek, 2nd best to use CVXQUAD, and worst to use neither. But none of those options will fix SCA. If there is a “bordeline” problem, Mosek or CVXQUAD might succeed, whereas not succeed without them. But for many SCA problems, all solver options will result in failure.
I see, then what should I do?
As I wrote above "Perhaps you should consider trying to use a non-convex solver under YALMIP…
if the point of your work is that you need to use a fancy algorithm, rather than using an off-the-shelf optimization solver, that is a matter for you to work out with your advisor. I come from the standpoint of the person seeking help wanting to solve a real world problem, not with the goal of having a novel paper to publish.
Just wanna to clarify, the “comvexifying” you mentioned previously, does it mean “convexifying”?
Then why you said this is where non-convexity arises? I am “convexifying” the problem right?
if your original problem was convex, you wouldn’t have to call CVX in a loop. You’d call it once and be done. You’re taking what should be an optimization variable, q, and making it indirectly part of the input data instead.
Hahaha, my project is not about developing a fancy algorithm useless I have to. So far my project is to repeat what has been done in a paper, and the problem I am dealing with is one optimization problem within the paper which has been published.
Even the slightest difference between what was done in the paper and what you did could be the difference between success and failure. Success or not can depend on the exact input data used, including which random numbers were drawn. It could also depend on stating value of q. . It might also be that undocumented behind the scenes tricks were used in the paper, or that the paper is flat out wrong. That happens a lot even in fairly prestigious journals.
I’m sorry about not making the problem clear, the original problem is not convex. But if you remember I said for each iteration I have two subsections, one is about vector u, and the other one is about vector q. I can guarantee, for each of these subsections/subproblems they are convex, and the first one always has an analytical solution by using Rayleigh Quotient method, and the second one can always been written in a GP form. That’s why I have to call CVX GP again and again.