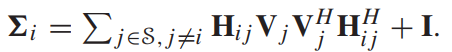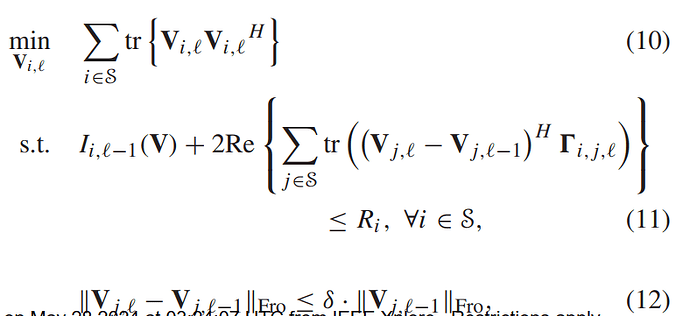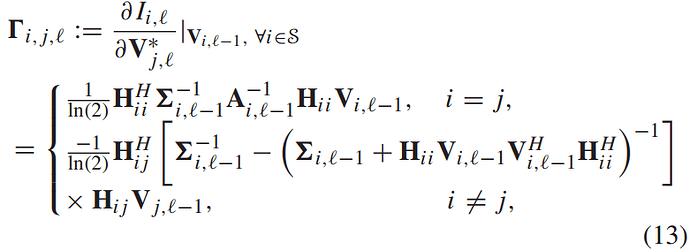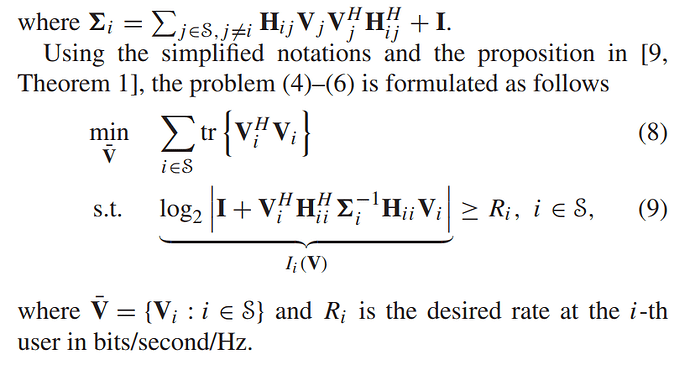Equation:
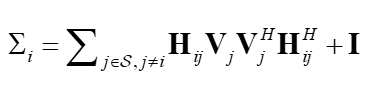
How to program this formula?
Error location: Sigma_i{i} = Sigma_i{i} + H_ij{i, j} * V_i{j} * V_i{j}’ * H_ij{i, j}';
Error message: Disciplined convex programming error:
Only scalar quadratic forms can be specified in CVX
Matlab code:
% -------- 基站 --------
M0 = 2 ; % 基站发射天线数量
N0 = 2 ; % 基站接收天线数量
% -------- 上行 UL --------
K = 2 ; % 上行UL用户数量
Mk = 2 ; %上行用户的天线数量
d_kUL = 2 ; % 上行数据流数量
% -------- 下行 DL --------
J = 2 ; % 下行DL用户数量
Nj = 2 ; % 下行用户的天线数量
d_jDL = 2 ; % 下行数据流数量
% 上行-下行用户 索引
S_UL = 1:K ; % 上行用户
S_DL = K+1:K+J ; % 下行用户
%% 上行信道+下行信道+自干扰信道+用户间信道CCI
H_kUL = cell(K,1) ; % 上行信道
for k_index = 1:K
h_UL = sqrt(1/2) * ( randn(N0, Mk) + 1i * randn(N0, Mk) ) ;
H_kUL{k_index,:} = h_UL ;
end
H_jDL = cell(J,1) ; % 下行信道
for j_index = 1:J
h_DL = sqrt(1/2) * ( randn(Nj, M0) + 1i * randn(Nj, M0) ) ;
H_jDL{j_index,:} = h_DL ;
end
% -------- 自干扰信道 --------
H0 = sqrt(1/2) * ( randn(N0, M0) + 1i * randn(N0, M0) ) ;
% -------- 上行用户-下行用户之间的干扰信道CCI --------
H_jkDU = cell(J,K) ;
for j_index = 1:J
for k_index = 1:K
h_DU = sqrt(1/2) * ( randn(Nj, Mk) + 1i * randn(Nj, Mk) ) ;
H_jkDU{j_index,k_index} = h_DU ;
end
end
% 公式(6)下面Denoting的H_ij
H_ij = cell(K+J,K+J) ;
for i = 1:(K+J)
for j = 1:(K+J)
if ismember(i, S_UL) && ismember(j, S_UL)
% i,j均为UL
H_ij{i, j} = H_kUL{j,:} ; % 上行信道
elseif ismember(i, S_UL) && ismember(j, S_DL)
% i为UL, j为DL
H_ij{i, j} = H0 ; % 基站自干扰信道
elseif ismember(i, S_DL) && ismember(j, S_UL)
% i为DL, j 为UL
H_ij{i, j} = H_jkDU{i-K, j} ; % 上下行用户干扰信道CCI
elseif ismember(i, S_DL) && ismember(j, S_DL)
% i,j均为DL
H_ij{i, j} = H_jDL{i-K,:} ;% 下行信道
end
end
end
%% CVX
cvx_begin
% 定义CVX变量
% 上行UL预编码
variable V_kUL(Mk, d_kUL, K) complex
% 下行DL预编码
variable V_jDL(M0, d_jDL, J) complex
% 初始化 V_i 矩阵
V_i = cell(K+J, 1);
for i = 1:(K+J)
if ismember(i,S_UL) % i是上行用户
V_i{i,:} = V_kUL(:,:,i);
elseif ismember(i,S_DL) % i是下行用户
V_i{i,:} = V_jDL(:,:,i-numel(S_UL));
else
error('用户i不在定义的用户集合中')
end
end
%% 计算 Sigma_i 公式(7)
Sigma_i = cell(K+J, 1);
for i = 1:(K+J)
if ismember(i, S_UL) % 上行用户
N = N0 ;
elseif ismember(i, S_DL) % 下行用户
N = Nj ;
end
Sigma_i{i} = zeros(N, N);
for j = 1:(K+J)
if j ~= i
Sigma_i{i} = Sigma_i{i} + H_ij{i, j} * V_i{j} * V_i{j}' * H_ij{i, j}';
end
end
Sigma_i{i} = Sigma_i{i} + eye(N);
end
cvx_end