To formulate my optimization problem, I confront with the problem that I will appropriate you if advise me.
I don’t know how I can define the following formula to the cvx.
log(1+∑_i▒〖b_i^2 p_i^2 a)〗,
where b and p are the variables.
Best regards
I’m not sure how well your formula is being displayed. it appears to be log of a vector, which is a vector. But, in the simplified case in which there is only one term in the sum, the vector entries having variables squared change convexity when the squared variable crosses one. Therefore, unless there are other problem aspects you haven’t told us about (for instance, you only used the squared variables as squares, and not unsquared), this is a non-convex problem.
Dear Mark
Thank you for your reply. Kindly be informed that the variable p and b >=0.
Best Regards
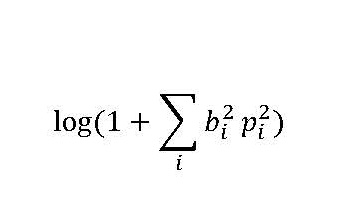
This is different than what I thought.
It is indefinite, i.e., neither convex nor concave, hence can not be handled by CVX. Consider the case in which there is only one term in the sum. Then, for instance, at b_1 = p_1 = 1, the Hessian of the function has one positive eigenvalue and one negative eigenvalue. Even if you are able to replace b_i^2 and p_i^2 by new variables representing their squares, the function would still be neither convex nor concave.
Thank you for your kind advises.