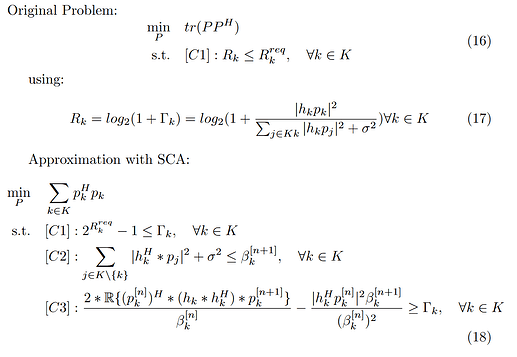Problem converging in CVX 1.22 but does not converge in CVX 2.22

[My_anonym_username]

Hi,

I have adopted a solution from this paper to solve a non-convex SDMA problem using SCA.

The original paper states that their SCA approximation should always converge to a local optimum, as only lower bound approximations are used.
I am pretty sure that my implementation should also have this property, as it uses exactly the same steps to construct the SCA problem.

“Convergence analysis: As (9), (11) and (12) are the lower bound approximations of (7d), (10a) and (8d), the optimal solution obtained in the [n − 1]-th iteration also serves as a feasible solution for the [n]-th iteration.”

The following is my Matlab implementation.

for cur_run = 1: max_runs
    cvx_begin quiet
        variable P_n1(NT,N_user) complex
        variable beta_n1(N_user,1)
        variable Gamma_n1(N_user,1)

        expression interf_ray(N_user,1)
        expression SINR_ray(N_user,1)

        % Define optimization variable
        trace_sum = 0;
        vector_ray= [];
        for k = 1:N_user
            p_k_n1 = P_n1(:,k);
            trace_sum = trace_sum+(p_k_n1'*p_k_n1);
        end


            % Construct constraints
            for k = 1:N_user
                p_k_n1 = P_n1(:,k);
                p_k_n = P_n(:,k);
                h_k = H(:,k);
                beta_k_n1 = beta_n1(k);
                beta_k_n = beta_n(k);

                % Sums up interfering users
                j_sum = 0;

                % Subloop building interference sum
                for j = 1:N_user

                    % Interfering user j 
                    p_j_n1 = P_n1(:,j);

                    if(k == j)
                        continue
                    else
                        % Note: We need to use square_pos here, which 
                        % corresponds to: x+=max{0,x}. 
                        % Regular square does not work
                        j_sum = j_sum + square_pos(abs(h_k'*p_j_n1));
                    end
                end

                % Array representing interference term
                interf_ray(k,1) = j_sum + sigma_n^2;

                % Array representing signal of interrest term
                SINR_ray(k,1) = 2*real(p_k_n'*(h_k*h_k')*p_k_n1)/beta_k_n ...
                    - (square_pos(abs(h_k'*p_k_n))*beta_k_n1)/(beta_k_n^2);
            end
            
        % Define optimization problem to solve
        minimize(trace_sum)
        subject to 
            interf_ray <= beta_n1;
            SINR_ray >= Gamma_n1;
            2.^(R_req.')-1 <= Gamma_n1 ;
    cvx_end

    % Prepare for next iteration
    beta_n = beta_n1;
    P_n = P_n1;

    cur_sol = cvx_optval;
    if(abs(cur_sol - last_sol) <= e)
        break;
    else
        last_sol = cur_sol;
    end
end

However, this implementation works fine in CVX version 1.22 (Downloaded from the CVX website), using SDPT3 for random parameters.

But in CVX version 2.2.2 (Downloaded from Github), the implementation does not converge for my initial values (also taken from this paper), using SDPT3 or SeDuMi. I have also tried to tweak the parameters (i.e. initial values for P_n , beta_n or h or stricter/more lenient requirements for R_req), which did not help. I was unable to find a single converging case.

I have also tried CVX version 2.2 (Downloaded from the CVX Website (Standard bundle)) and tried using MOSEK, which also did not converge.

Does anyone had a similar problem recently and found a solution? Or does anyone see a problem with my model being incorrect and thus not converging?

[Mark_L_Stone]

Have you examined the nature of non-convergence? Is each subproblem solved to claimed optimality? Or perhaps numerical difficulties are encountered by the solver? Or eventually a subproblem is infeasible? Or all the subproblems are solved to claimed optimality, but optimal objective values cease improving, or perhaps start getting worse?

SCA can be very problematic. if the papers authors have a claim of convergence to a local optimum, perhaps you should further investigate, including with the paper’s aithors, and understanad the practical limitations.

[My_anonym_username]

Hi Mark,

I will take a look at the points that you have mentioned and then eventually followup the discussion with my findings.

Thanks for your input.

[My_anonym_username]

Hallo Mark,

I have tried to analyse my problem further, but I think I am lacking understanding of CVX and/or Convex optimization to find a solution on my own. Maybe you can help me out again

First I looked at the convergence. The statements of the original authors is in full length:

Convergence analysis: As (9), (11) and (12) are the lower bound approximations of (7d), (10a) and (8d), the optimal solution obtained in the [n − 1]-th iteration also serves as a feasible solution for the [n]-th iteration. Therefore, the corresponding optimal objective value WSR[n−1] is no larger than WSR[n]. Besides, the objective function is bounded by the transmit power constraint (6d), the convergence is hence guaranteed. However, there is no guarantee of the global optimality since a local optimum can also result in termination of the iteration process.

From my understanding this argument should be applicable to my problem as well: The Rate constraint (16) provides a lower bound to the objective function, as PP^H can not get infinitively small while still fulfilling (16) for R_{req} \neq 0. I would also argue that any optimal point produced in iteration [n] is also feasible in iteration [n+1], as it was produced by the optimization in the first place.This is by no means a proof, but as this seems logical to me. Additionally, CVX Version 1.22 produces the expected converging behaviour. Therefore, I personally would assumed that the convergence should be given, but maybe I am not rigorous enough here.

What I encounter in CVX:

• Version 1.22: CVX shows converging behaviour (objective value decreases constantly) over the iterations, when using the previous solution as the starting point for the iteration. The final optimal value is +0.73113 for a tolerance of e = 0.00001 between iterations.
• Version 2.2.2/2.2: The Algorithm produces a point far lower than the optimum of version 1.22 on the (optimal value: +0.349756) with a neglectable duality gap after several “back-and-forth” iterations. However, the next iteration -which uses the +0.349756 parameter set as a starting point- is then infeasible and yields no solution.

I think that this is somehow correlated - maybe the point corresponding to objective value +0.349756 was somehow not feasible in the first place? However, this can not be true, due to the small duality gap (at least from my understanding).

Maybe you have an idea what CVX version 2.2.2 does differently.

The full CVX Output of SDPT3:
Trace 1.22: CVX-Version: 1.22 - Pastebin.com
Trace 2.2.2: CVX-Version: 2.2.2 - Pastebin.com

Ps: The program involves no randomness. All parameters (such as h_k, the initial p_k, etc.) are set deterministically.

Cheers
BL

[Mark_L_Stone]

Maybe the claims in the paper are idealized, and not true in practice?