Problem about log(1+exp(x))

1

Hello, everyone! Thank you for your attention !
I have one problem about this expression, how to express it by CVX?
Variable : tao[n] , l1[n] and l2[n]

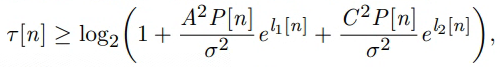
image

2

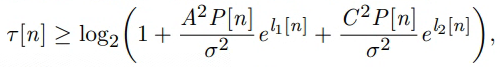
help log_sum_exp

log_sum_exp log(sum(exp(x))).
log_sum_exp(X) = LOG(SUM(EXP(X)).

When used in a CVX model, log_sum_exp(X) causes CVX's successive
approximation method to be invoked, producing results exact to within
the tolerance of the solver. This is in contrast to LOGSUMEXP_SDP,
which uses a single SDP-representable global approximation.

If X is a matrix, LOGSUMEXP_SDP(X) will perform its computations
along each column of X. If X is an N-D array, LOGSUMEXP_SDP(X)
will perform its computations along the first dimension of size
other than 1. LOGSUMEXP_SDP(X,DIM) will perform its computations
along dimension DIM.

Disciplined convex programming information:
    log_sum_exp(X) is convex and nondecreasing in X; therefore, X
    must be convex (or affine).

You will need to divide by log(2) because log_sum_exp is based on log, not log2.

Despite what the help says, CVX’s Successive Approximation method is not used if CVX 2.2+Mosek9.x or 10.x are used (preferred), or if CVXQUAD’s exponential.m replacement is used (2nd choice to use of CVX 2.2 + Mosek 9.x or 10.x)

3

Thank you for your reply very much!
According to your suggestion, I transform the constraint as follows:

X=[ ln(sigma/P[n])， 2log(A)+l1(n)， 2log（C)+l2(n) ]
tao(n)*log(2) >= log(P(n)/sigma) +log_sum_exp(X);

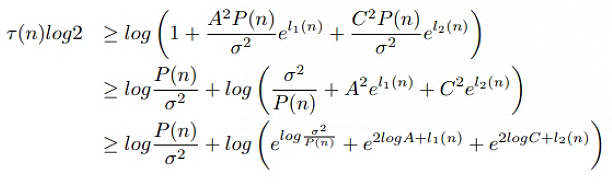
image

4

I think you got it right, except in the first element of X, you forgot to square sigma, or multiply the log by 2, And of course the ln in that element should be log.

5

Yes, thank you for your reminder. Thank you very much !