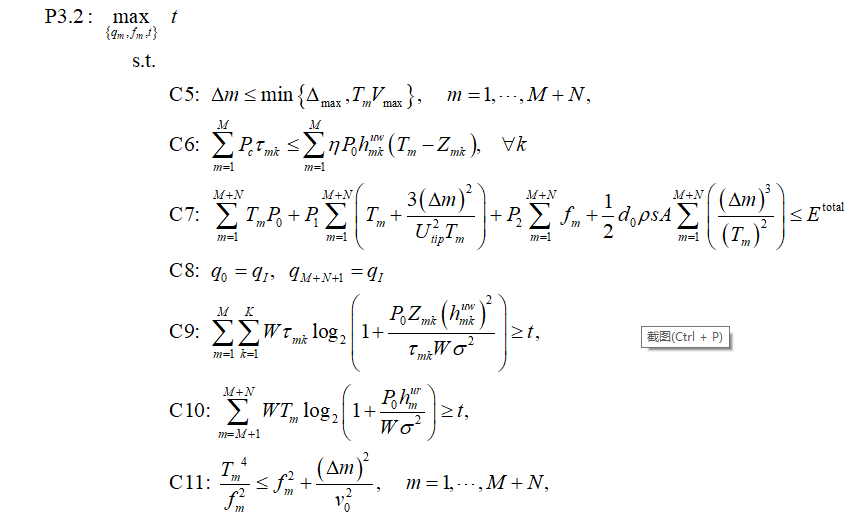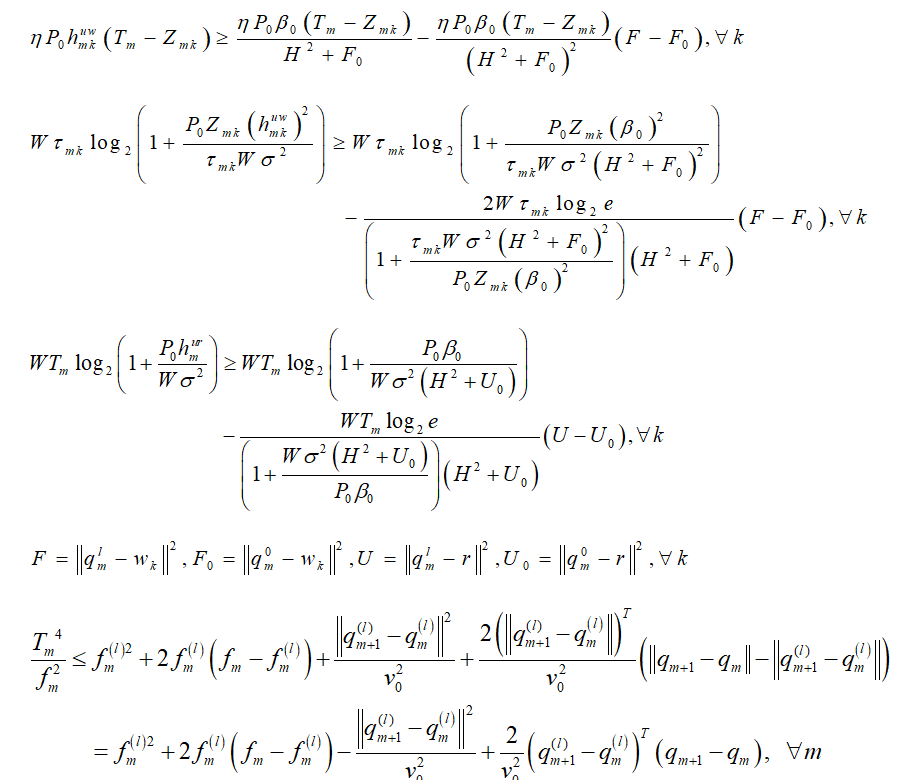Please help me !How to explain the following phenomenon in CVX?

1

Why is the equal sign not satisfied sometimes in

F(m,k)=((X(m)-W(k,1))^2+(Y(m)-W(k,2))^2)；

U(m,1)=((X(m)-r(1))^2+(Y(m)-r(2))^2);

delta(m,1)=(X(m+1)-X(m))^2+(Y(m+1)-Y(m))^2;

The entire program is shown as

cvx_begin
variables X(M+N+1,1) Y(M+N+1,1) t f(M+N,1)
expressions F U delta EH1 EH2 EE1 EE2 EE3 EE4 R_BB1 R_BB2 R_FF1 R_FF2
maximize t
subject to
%F
for m=1:M
    for k=1:K
        F(m,k)=((X(m)-W(k,1))^2+(Y(m)-W(k,2))^2);
    end
end
%F0
for m=1:M
    for k=1:K
        F0(m,k)=(X0(m)-W(k,1))^2+(Y0(m)-W(k,2))^2;
    end
end
%U
for m=M+1:M+N
    U(m,1)=((X(m)-r(1))^2+(Y(m)-r(2))^2);
end
%U0                                                          
for m=M+1:M+N
    U0(m,1)=(X0(m)-r(1))^2+(Y0(m)-r(2))^2;
end
%delta0^2
for m=1:M+N
   delta0(m,1)=(X0(m+1)-X0(m))^2+(Y0(m+1)-Y0(m))^2;
end
%delta^2
for m=1:M+N
   delta(m,1)=(X(m+1)-X(m))^2+(Y(m+1)-Y(m))^2;
end
%C5
delta<=(min(delta_max,T.*Vmax)).^2;
%C6
for k=1:K
EH1=yita*P0*beita0*(T(1:M,1)-Z(:,k))./(H^2+F0(:,k));
EH2=-yita*P0*beita0*(T(1:M,1)-Z(:,k)).*(F(:,k)-F0(:,k))./((H^2+F0(:,k)).^2);    
sum(Pc*tao(:,k))<=sum(EH1+EH2);
end
%C7
EE1=sum(P0*T);
EE2=P1*sum((T+3*delta./((Utip^2)*T)));
EE3=sum(P2*f);
EE4=(1/2)*d0*rou*s*A*sum(pow_pos(delta,3/2)./(T.^2));
EE1+EE2+EE3+EE4<=E_total;
%C8
X(1)==q0(1);Y(1)==q0(2);X(M+N+1)==qI(1);Y(M+N+1)==qI(2);
%C9
R_BB1=sum(sum(B*tao.*log(1+P0.*Z*beita0*beita0./(tao*B*N0.*(H^2+F0).^2))/log(2)));
R_BB2=sum(sum(-2*B*tao.*(F-F0)./((1+(tao*B*N0.*(H^2+F0).^2)./(P0*Z*beita0*beita0)).*(H^2+F0)*log(2))));
R_BB1+R_BB2>=t;
%C10
R_FF1=sum(B*T(M+1:M+N,1).*log(1+P0*beita0./(B*N0*(H^2+U0(M+1:M+N,1))))/log(2));
R_FF2=sum(-B*T(M+1:M+N,1).*(U(M+1:M+N,1)-U0(M+1:M+N,1))./((1+(B*N0*(H^2+U0(M+1:M+N,1)))./(P0*beita0)).*(H^2+U0(M+1:M+N,1))*log(2)));
R_FF1+R_FF2>=t;
%C11
(T.^4).*pow_pos(inv_pos(f),2)<=(f0).^2+2*(f0).*(f-f0)-delta0/(v0^2)+2/(v0^2)*(X0(2:M+N+1,1)-X0(1:M+N,1)).*(X(2:M+N+1,1)-X(1:M+N,1))+(Y0(2:M+N+1,1)-Y0(1:M+N,1)).*(Y(2:M+N+1,1)-Y(1:M+N,1));
cvx_end

The above program is to solve the following optimization problem,

1687686327711
1687686327711864×515 15 KB

To deal with the non-convex terms in C6, C9, and C10, SCA technique is applied, i.e.,

1687686523200
1687686523200908×780 21.4 KB

2

if CVX completes successfully, all CVX variables are at their optimal value after CVX concludes.

However, this is not necessarily so for CVX expressions, which includes anything on the LHS of =, whether declared as an expression or not. So to get the optimal values,F, U, delta need to be calculated after cvx_end, starting with optimal values of CVX variables.

This is due to a design decision in CVX, which I suppose sometimes saves some calculation, but at the expense of confusion.

3

Thanks for your explanation!

However, there are still the following questions for me.

If the LGS of = can include anything for CVX expressions, will the use of CVX expressions in constraints affect the optimal solutions?

Specifically, for

R_BB1=sum(sum(B*tao.*log(1+P0.*Z*beita0*beita0./(tao*B*N0.*(H^2+F0).^2))/log(2)));
R_BB2=sum(sum(-2*B*tao.*(F-F0)./((1+(tao*B*N0.*(H^2+F0).^2)./(P0*Z*beita0*beita0)).*(H^2+F0)*log(2))));
R_BB1+R_BB2>=t;

R_FF1=sum(B*T(M+1:M+N,1).*log(1+P0*beita0./(B*N0*(H^2+U0(M+1:M+N,1))))/log(2));
R_FF2=sum(-B*T(M+1:M+N,1).*(U(M+1:M+N,1)-U0(M+1:M+N,1))./((1+(B*N0*(H^2+U0(M+1:M+N,1)))./(P0*beita0)).*(H^2+U0(M+1:M+N,1))*log(2)));
R_FF1+R_FF2>=t;

If F, U can be any value, will it not affects the optimal value of t.

4

The expressions should have the correct optimal values internally in CVX and the solver. But they have to be recalculated starting from CVX optimal variable values if you want to know what they are. I.e., the optimization problem should be correctly solved whether or not it uses expressions.