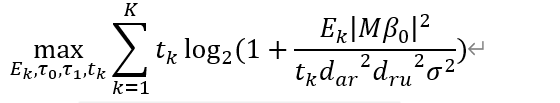Please!help me! About cvx expression

1

Pa = 500;
H_u = 30;
H_a = 10;
K = 3;
M = 50;
beta0 = 10^(-6);
sigma = 10^(-67/10)*1e-3;
q_u = [245 255]‘;
q_k = [70 400; 88 310; 143 383]’;
q_a = [0 0]';
for k = 1:K
d_ru(k,1) = sqrt(norm(q_u - q_k(:,k))^2 + H_u^2);
d_ar(k,1) = sqrt(norm(q_u - q_a)^2 + (H_a - H_u)^2);
end

cvx_begin
variable E(K)
variable tau0
variable tau1
variable t(K)
rate = 0;
for k = 1:K
rate = rate + t(k) * (log(1 + E(k) * (abs(M * beta0)^2) ./ (t(k) * d_ar(k,1)^2 * d_ru(k,1)^2 * sigma)) ./ log(2));
end
maximize(rate)
subject to
E <= tau1 * eta * Pa * (abs(M * beta0)^2) / (d_ar^2 * d_ru^2);
tau0 + tau1 + sum(t) <= 1;
for k = 1:K
E(k) >= 0;
t(k) >= 0;
end
tau0 >= 0;
tau1 >= 0;
cvx_end

It has error following:
错误使用 .* (line 173)
Disciplined convex programming error:
Cannot perform the operation: {real affine} ./ {real affine}

出错 ./ (line 19)
z = times( x, y, ‘./’ );

出错 luck (line 23)
rate = rate + t(k) * (log(1 + E(k) * (abs(M * beta0)^2) ./ (t(k) * d_ar(k,1)^2 * d_ru(k,1)^2 *
sigma)) ./ log(2));

2

DBM83KFXAL8MTZ8OX@@`)A7

this is “rate” expression.please help me look for where this expression is written incorrectly.Thank you very very much!

3

t*log2(1+y/t) = -rel_entr(t,t+y)/log(2). The latter of which will be accepted by CVX.

If t and y are both vectors of the same dimension, you can use
sum(-rel_entr(t,t+y)/log(2))

y(k) would be all the stuff multiplying 1/t(k)

4

Okay, thank you very much. I’ll try as you say.thanks again.