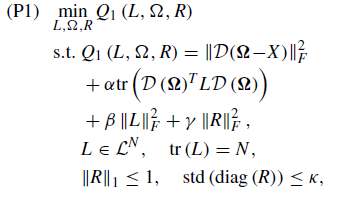![]()
Given the cost function in the picture above I need to minimize this such that norm(R,1)<=1 and std(diag(R))<=0.1
my initialization for the R matrix is an identity matrix so after the optimization I must obtain a matrix that is as close as the identity matrix.
D(X) is a difference operator given by the D(X)=X-RXB.
Here is the function I made:
function R=RLearning(R,alpha,gamma,kappa,X,L,B)
N=max(size(R));
[numnode,numhour]=size(X);
gamma=1e-3;
kappa=kappa;
% Obj_var=alpha*trace(transpose(X)*L*X)+gamma*(norm(R,'fro'))^2;
Obj_var=norm(Diff(X,R,B),'fro')^2+alpha*trace(transpose(Diff(X,R,B))*L*Diff(X,R,B))+norm(L,'fro')+gamma*(norm_nuc(R-eye(N)))^2;
cvx_precision high;
cvx_begin
variable R(numnode,numnode) diagonal
% variable L(numnode,numnode)
% variable X(numnode,numhour)
% variable B(numhour,numhour)
minimize(Obj_var)
subject to
norm(R,1)<=1;
%issymmetric(Z);
std(diag(R))<=kappa;
%trace(Z)==N;
% R==eye(N);
cvx_solver_settings('dumpfile', 'cvx_debug.txt');
cvx_solver_settings('max_iters', 100);
% dumpfile_contents = fileread('cvx_debug.txt');
% disp(dumpfile_contents);
cvx_end
disp('Optimization finished.');
disp(['Exit status: ' cvx_status]);
disp(['Objective function value: ' num2str(Obj_var)]);
disp(['Number of iterations: ' num2str(cvx_slvitr)]);
disp(['Convergence tolerance: ' num2str(cvx_slvtol)]);
difference_term = Diff(T, R, B);
frobenius_term = norm(difference_term, 'fro')^2;
trace_term = alpha * trace(transpose(difference_term) * L * difference_term);
nuclear_term = gamma * norm_nuc(R - eye(numnode))^2;
disp(['Frobenius norm term: ' num2str(frobenius_term)]);
disp(['Trace term: ' num2str(trace_term)]);
disp(['Nuclear norm term: ' num2str(nuclear_term)]);
scaled_R = 0.7 * eye(size(R));
scaling_factor = norm(scaled_R, 'fro') / norm(R, 'fro');
adjusted_R = scaling_factor * R;
disp(['Scaling Factor: ' num2str(scaling_factor)]);
disp('Adjusted R:');
disp(adjusted_R);
end
I tried several times but the results I procure are 0.3s scaled to 1e-14 values in the optimized R matrix. Please let me know where there is an issue and how do I track and fix it.
These are the results that I am getting
Optimization finished.
Exit status: Solved
Objective function value: 235.7059
Number of iterations: 26
Convergence tolerance: 1.6851e-12
Frobenius norm term: 480264
Trace term: 1910.89
Nuclear norm term: 625
R
R =
1.0e-14 *
(1,1) 0.3144
(2,2) 0.3144
(3,3) 0.3144
(4,4) 0.3144
(5,5) 0.3144
(6,6) 0.3144
(7,7) 0.3144
(8,8) 0.3144
(9,9) 0.3144
(10,10) 0.3144
(11,11) 0.3144
(12,12) 0.3144
(13,13) 0.3144
(14,14) 0.3144
(15,15) 0.3144
(16,16) 0.3144
(17,17) 0.3144
(18,18) 0.3144
(19,19) 0.3144
(20,20) 0.3144
(21,21) 0.3144
(22,22) 0.3144
(23,23) 0.3144
(24,24) 0.3144
(25,25) 0.3144