Dear everyone,
My code is followed,
clear;
clear all;
k = 8; % The number of user in a small cell
PL = 0;
r = ones(1,k);
%Simulation parameters
n = 0.3; % shared fraction, 0<=n<=1
N0 = 1e-5; % noise power spectral density(dBm/Hz)
%N0 = power(10,N0/10)/1000; % Converted to w/Hz
Wul = 1e6; Wdl = 1e6; % The uplink and downlink bandwidth (Hz)
Pumax = 100; Pdmax = 1000; % The uplink and downlink power(w)
FC = 10^8; % The cloudlet server processing capacity(CPU cycles/s)
luk = 1.7810^-6; % The amount of energy spent by the mobile device to extract each bit of offloaded data from the video source(J/bit)
ldk = 0.625; % Parameter that captures the mobile receiving energy expenditure per second in the downlink(J/s)
BIk = 1e4ones(1,k); % Input bits from each user k to the cloudlet in the uplink (1Mbits)
BOk = 1e4ones(1,k); % Out bits from the cloudlet to each user k in the downlink (1Mbits)
%Vk = 2640BIk; % Processing the input BIk by executing Vk CPU cycles at the cloudlet (CPU cycles)
%Vs = nVk; % Shared CPU cycles
BOs = nBOk; % Shared output bits that delivered to all users
BIs = n*BIk; % Shared input bits that can be sent by any of the users
%Initialize the z = [Pul,Bls,f,Pdl,PdM,TuS,TdS]
Pulk0 = Pumaxrand(1,k); % The uplink power(w)of user k
%Pdlk0 = Pdmax/kones(1,k); % The downlink power(w)to user k
Pdlk0 = rand(1,k);
Pdlk0 = Pdlk0/(sum(Pdlk0))Pdmax;
PdlM0 = Pdmaxrand(1,1); % Transmit power (w) for multicasting
%BIsk0 = BIs/k.*ones(1,k); % A fraction of BIsk bits of the BIs shared bits transmited by user k
BIsk0 = rand(1,k);
BIsk0 = BIsk0/sum(BIsk0).*BIs;
fk0 = rand(1,k);
fk0 = fk0/(sum(fk0));
fs0 = rand(1,1); % Fractions of the processing power FC assigned to run the Vk CPU cycles exclusively for user k and the VS shared CPU cycles
f0 = [fk0,fs0];
Vk = 2640*(BIk-BIsk0+BIs);
Vs = 2640*BIs;
PU0 = r.(Pulk0-PL); % The uplink power after rayleigh fading
Rulk0 = (Wul/k)log2(1+PU0/(N0Wul/k)); % Transmitting rate of user k in the uplink
PD0 = r.(Pdlk0-PL); % The downlink power after rayleigh fading
Rdlk0 = (Wdl/k)log2(1+PD0/(N0Wdl/k)); % Transmitting rate to user k in the downlink
PM0 = r.(PdlM0-PL); % Multicasting power after rayleigh fading
RdlMk0 = Wdllog2(1+PM0/(N0*Wdl)); % Transmitting rate to users for multicasting
TuS0 = max(BIsk0./Rulk0); % The time to complete the shared uplink transmissions (s)
TdS0 = max(BOs./RdlMk0); % The downlink transmission time to multicast BOs bits
Tmax = 2; % Maximum latency constraint(0.15s/0.05s)
z0 = [Pulk0,BIsk0,f0,Pdlk0,PdlM0,TuS0,TdS0];
alpha = 10^-5; epsilong = 10^-5; delta0 = rand; % Accuracy parameters
%cvx_solver SeDuMi
%cvx_solver ecos
%cvx_solver mosek
cvx_begin
variables Pulk(1,k) BIsk(1,k) fk(1,k) fs Pdlk(1,k) PdlM TuS TdS;
f = [fk,fs];
PU = r.*(Pulk-PL);
Rulk = (Wul/k)*log(1+PU/(N0*Wul/k))/log(2);
PD = r.*(Pdlk-PL);
Rdlk = (Wdl/k)*log(1+PD/(N0*Wdl/k))/log(2);
PM = r.*(PdlM-PL);
RdlMk = Wdl*log(1+PM/(N0*Wdl))/log(2);
%The overall downlink mobile energy consumption for user k
Edlk = ((BOk-BOs).*inv_pos(Rdlk)+(BOs.*inv_pos(RdlMk)))*ldk;
%Mobile energy consumption of uplink transmission
z = [Pulk,BIsk,f,Pdlk,PdlM,TuS,TdS];
% E = (z-z0)diag(z0)(z-z0)’;
e1 = Pulk0.(BIsk0+(BIk-BIsk0)).inv_pos(Rulk);
e2 = Pulk0.(BIsk+(BIk-BIsk0))./Rulk0;
e3 = Pulk.(BIsk0+(BIk-BIsk0))./Rulk0;
e4 = luk*(BIsk+(BIk-BIsk0));
Eulk = e1+e2+e3+(z-z0)diag(z0)(z-z0)’+e4;
% Rewrite the latency constraints C.2
g1 = square_pos(BIsk+inv_pos(Rulk));
g2 = Rulk0.*Rulk0;
g3 = (g1-BIsk0.^2-1./g2);
g4 = BIsk0.*(BIsk-BIsk0);
g5 = (r.*Pulk0)/(N0*Wul/k);
g6 = (1+g5).*(Rulk0.^4);
g7 = g4-(Rulk0./g6).*(inv_pos(Rulk)-1./Rulk0);
gk = 1/2*g3-g7;
minimize(sum(Eulk+Edlk))
subject to
(BIk - BIsk0).*inv_pos(Rulk)+(Vk-Vs)/FC.*inv_pos(fk)+Vs/FC*inv_pos(fs)+(BOk-BOs).*inv_pos(Rdlk) <= Tmax-TuS-TdS; % Constraint C.1
gk < TuS; % Constraint C.2
BOs.*inv_pos(RdlMk) <= TdS; % Constraint C.3
sum(fk) == 1; % Constraint C.4
0 < fk;
0 <= fs < 1;
sum(BIsk) == BIs; % Constraint C.5
sum(Pdlk) <= Pdmax; % Constraint C.6
10^-5 < Pdlk <= Pdmax;
10^-5 < PdlM <= Pdmax;
10^-5 < Pulk <= Pumax;
0 <= TuS <= Tmax;
0 <= TdS <= Tmax;
0 <= BIsk <= BIs;
cvx_end
In my code, the object function is min(sum(Eulk+Edlk)), and Eulk = e1+e2+e3+(z-z0)diag(z0)(z-z0)’+e4, Edlk = ((BOk-BOs).*inv_pos(Rdlk)+(BOs.*inv_pos(RdlMk)))*ldk. The result I got followed:
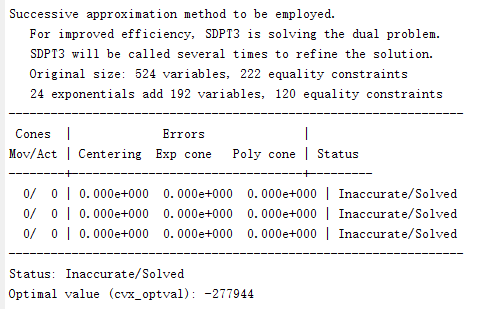
The optimal value obtained by cvx directly is not the sane as the result calculated by optimal solution.
Why did the result happen?
Thank you. 

