Nuclear Norm problem

1

Hello friends!

I hope you are all doing great and staying safe!
This has been a very helpful and engaging community!

So, I have been battling with a problem lately but have not been able to find a solution yet. I believe I must be doing something wrong when translating the math into Matlab. Here is the situation.

I have a complex matrix that contains some observed data points and some that are missing, which are filled with NaN in Matlab. This matrix has to be Hermitian and positive semidefinite, which is a requirement for the problem. I am trying to complete the matrix (i.e. find the unobserved entries) by minimizing the nuclear norm subject to some constraints. Mathematically, this is:

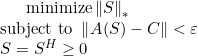
CodeCogsEqn

Here, the operator A(S) just extracts the known elements. It is included to avoid changing the observed points. So, the nuclear norm of S has to be minimized, subject that the below conditions. I have expressed this in matlab as:

mmm=~isnan( C );
cvx_begin
variable X(N,N) hermitian semidefinite
minimize (norm_nuc(X))
subject to
norm(X(mmm)-aux(mmm))<= epsilon
cvx_end

However, the code does not seem to do what I want. Instead, it just places zeros where the original unobserved values are located. Do you have any suggestions?

Thank you and take care you all :slight_smile:
David

2

It works for me on a toy example (I presume you meant C rather than aux in the constraint). The filled in entries were not zero.

But it might be slightly better to change the constraint to
X(mmm) == C(mmm)

Can you show a minimum reproducible example, for instance with N = 3, which exhibits the incorrect behavior you experienced?

However, note that the optimal solution need not be unique, and all NaN elements being zero might be optimal (or an optimum). You might want to re-think how well this methodology suits your purpose of determining the missing elements, if they are not uniquely determinable by your proposed methodology.

Using this simple example:
C=[4 NaN 2;NaN 3 1;2 1 5];
(which was the first semi-random example I made up),`the optimal objective value = 12, and can be achieved with any real value of NaN elements from -2.59333 to 3.39333. So big time non-uniqueness.