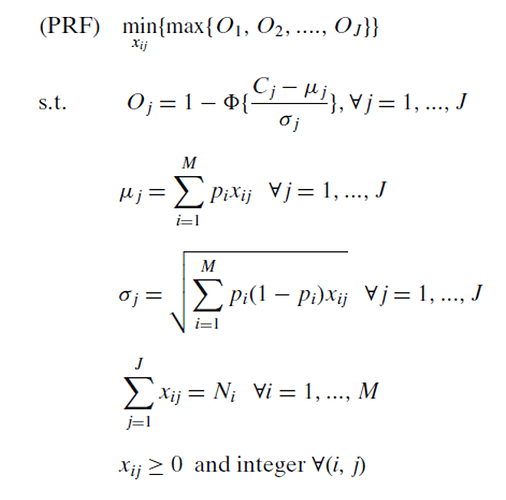Need some help with my code

Nonconvex
1

I’m using CVXR for the first time today, to perform a minimization of a max of a set of variables.

So i set my objective function as:

O_j <- Variable(20)
objective <- Minimize(max_entries(O_j))

So this should minimise the maximum of the 20 O_j values, as I understand it from the CVXR documentation.

Now in defining constraints, I am having issues in defining sets of constraints. Since I have 20 variables (and 2 more sets of 20 variables, which are mu_j and sigma_j), defining 20 constraints line by line is obviously tedious, and I am sure there is some way of aggregating this, for constraints that work by the universal quantifier/for all.

for example, one constraint is:

O[j] = 1-pnorm((C([j] -mu[j])/sigma[j])

for all j=1,2,3…20 (C is a constant vector of length 20)

I can replace the generic pnorm in R with p_norm in CVXR. But how will I aggregate all 20 constraints in one line of code? I’m new to using this package so I’m a bit confused.

Additionally, can functions like sqrt be used in constraints the same way or is there an equivalent for CVXR? I have a constraint which is:

sigma[j] = sqrt(sum(P[i] * (1 - P[i]) * X[i,j] )

for all j = 1,2,3…20. Here, P is a constant vector of length 30. X is a variable defined as Int(30,20)

Now the sum here works like the excel function SUMPRODUCT(), that is,

P[1] * (1-P[1]) * X[1,j] + P[2] * (1-P[2]) * X[2,j] + … + P[30] * (1-P[30]) * X[30,j]

I would normally do this using dplyr if I knew the values of X[ i , j ]. Will sum_entries work here?

The code works fine if I define each constraint line by line, but there must be a more efficient way to do this right? I know these doubts are pretty basic but I’m just starting to learn how to code with R/CVXR and any help would be appreciated. Thanks.

1 Like
2

This is not the Forum for CVXR but CVX for Matlab. Maybe you ended up in the wrong place by mistake.

3

alright, can a similar thing be done in MATLAB then? I am just unable to find any forum for CVXR

4

If you wish to use CVX (under MATLAB), feel free to ask on this forum. Note that if you are familiar with MATLAB, you should be able to figure out how to vectorizec constraitns and expressions in "one line of ciode, which do the extent you can do so, usually speeds up the CVX processing. But you can always use for loops if you have to, or don’t care about CVX processing time.

5

So I’ll just post the formulation here, if you could just help me with 2 things I can figure out the rest.

Formulation
Formulation.PNG625×617 60 KB

So here, the objective function is easy enough to code. How would I do constraint number 1 and 3 now? As you can see:

  1. With constraint 1, it has the phi function, which is the normpdf() function in regular MATLAB. How would I do that in the CVX constraint definition syntax?
  2. With constraint 3, I have matrix X(i,j) which is a 30x20 matrix of variables, which while not present in the objective function are the decision variables of the optimisation. There are 20 constraints, and the summation takes the 30 values of each column in the product. P(i), N(i) and C(j) are constants which I already have. So how would I vectorise this while only taking the sum of each column(times each constant, of course)
6

Don’t start off worrying about vectorization, worry about whether the optimization problem is convex. It doesn’t look convex to me.

What you call constraints 1 through 3 are better thought of as being expression assignments (they woould be a total no-go as constraints because nonlinear equality constraints are not allowed by CVX or CVXR).

CVX does have a concave approximation for the log of the standard normal distribution function,log_normcdf. Note that you would use normcdf, not nomrpdf, in MATLAB because \Phi is the cdf, not pdf of a standard Normal. However, \sigma_j is a concave function of x_{ij} and I don’t believe that (C_j - \mu)/\sigma_j would be a concave argument needed to use log_normcdf. So even though you could take the log of the objective function, I believe you are out of luck with \Phi((C_j - \mu_j)/\sigma_j) in CVX and I suspect all other DCP type modeling toolds such as CVXR.

If you can come up with a convex formulation of your problem, or at least a good enough convex approximation, then perhaps you could use CVX. Otherwise, you may need to use a non-convex optimizer.

help log_normcdf

log_normcdf Logarithm of the cumulative normal distribution.
Y = log_normcdf(X) is the logarithm of the CDF of the normal
distribution at the point X.

                             1    / x
    log_normcdf(X) = LOG( ------- |   exp(-t^2/2) dt )
                          sqrt(2) / -Inf

For numeric X, log_normcdf(X) is computed using the equivalent 
expression LOG(0.5*ERFC(-X*SQRT(0.5))). When X is a CVX variable, a 
a piecewise quadratic *approximation* is employed instead. This
approximation gives good results when -4 <= x <= 4, and will be
improved in future releases of CVX.

For array values of X, the log_normcdf returns an array of identical
size with the calculation applied independently to each element.

X must be real.

Disciplined convex programming information:
    log_normcdf is concave and nondecreasing in X. Therefore, when used
    in CVX specifications, X must be concave.

help cvx.max

Disciplined convex/geometric programming information:
    max is convex, log-log-convex, and nondecreasing in its first 
    two arguments. Thus when used in disciplined convex programs, 
    both arguments must be convex (or affine). In disciplined 
    geometric programs, both arguments must be log-convex/affine.