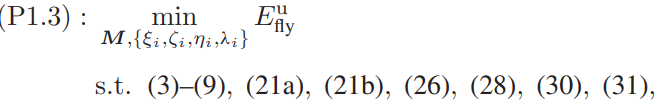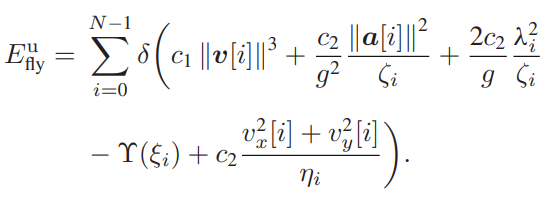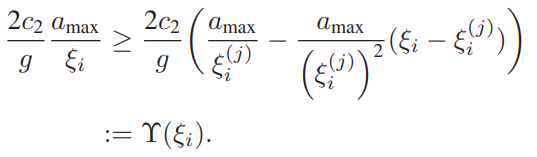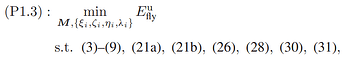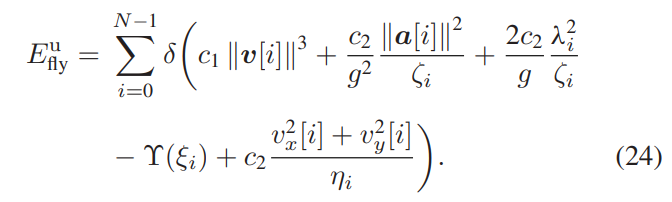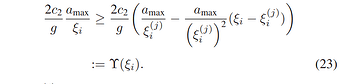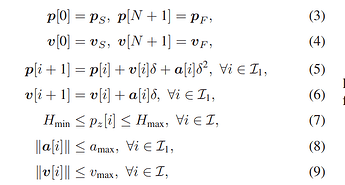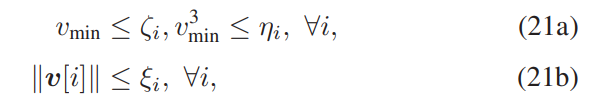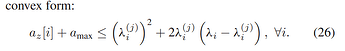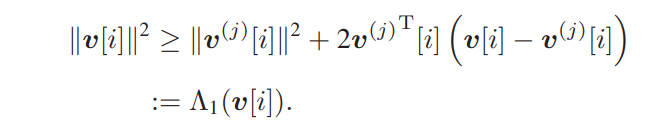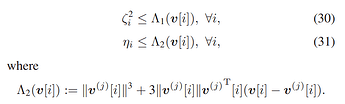Need Help on quad_over_lin

[Amirhossein_Solati]

Hi,

I would like to write the following formula in MATLAB. I have implemented the formula, but I’m not sure if I used “quad_over_lin” correctly. I would appreciate your help. Here is the formula and the code I have written:

E = 0;
for n = 1:N
    efly = delta*(c1*pow_pos(norm(v(:,n)),3) + c2*0.01*quad_over_lin(a(:,n),zeta(n)) ...
        + 2*c2*0.1*quad_over_lin(landa(n),zeta(n)) - Aux2 +c2*quad_over_lin(v(1,n),eta(n)) + c2*quad_over_lin(v(2,n),eta(n)));
    E = E + efly;
end

here v and a are 3x400 where v = [ vx,vy,vz] and zeta and eta are auxiliary
variables and are 1x400 nonnegative and c1,delta,c2 andg are constants

[Mark_L_Stone]

It looks correct.

If N is large and you want to speed up the CVX processing, I think you should be able to eliminate the for loop, and instead vectorize. Do so by using norms and the vector form of quad_over_lin.

help quad_over_lin

quad_over_lin Sum of squares over linear.
Z=quad_over_lin(X,Y), where X is a vector and Y is a scalar, is equal to
SUM(ABS(X).^2)./Y if Y is positive, and +Inf otherwise. Y must be real.

If X is a matrix, quad_over_lin(X,Y) is a row vector containing the values
of quad_over_lin applied to each column. If X is an N-D array, the operation
is applied to the first non-singleton dimension of X.

quad_over_lin(X,Y,DIM) takes the sum along the dimension DIM of X.
A special value of DIM == 0 is accepted here, which is automatically
replaced with DIM == NDIMS(X) + 1. This has the effect of eliminating
the sum; thus quad_over_lin( X, Y, NDIMS(X) + 1 ) = ABS( X ).^2 ./ Y.

In all cases, Y must be compatible in the same sense as ./ with the squared
sum; that is, Y must be a scalar or the same size as SUM(ABS(X).^2,DIM).

Disciplined convex programming information:
    quad_over_lin is convex, nonmontonic in X, and nonincreasing in Y.
    Thus when used with CVX expressions, X must be convex (or affine)
    and Y must be concave (or affine).

[Amirhossein_Solati]

Thanks Mark For your answer, I got unbounded status so I wondered if Cost Function is correct or not Maybe I should care about Constraints or initial values. is it ok to assign initial value as ones[1, N+1] or zeros[1,N+1]. Could you please give advise on how to initialize parameters correctly?, I mean generally

[Mark_L_Stone]

Input data to CVX us initialized (set) per whatever is allowed in MATLAB. CVX variables are never initialized, because their optimal values are determined by the solver (note that some mixed-integer and non-convex solvers allow starting values, but not in CVX).

If you are calling CVX iteratively, as in SCA, then you need to set starting values for those “variables” which are treated as being input data for each CVX optimization problem.

You can read Debugging unbounded models - YALMIP, which also applies to CVX.

[Amirhossein_Solati]

Yes The Algorithm is SCA and after finding the optimal value, those initialed values must be replaced with optimal value.
Thanks for your Consideration and Time.

[Mark_L_Stone]

The result obtained using the SeDuMi solver is inaccurate. The optimal solution is not as good as before the optimization.

Unsafeguarded (no line search or trust region)Successive Convex Approximation (SCA) or generally, alternating variables optimization are unreliable. It might not descend (for minimization problem), i.e., iterates could get worse. It might not converge to anything; and if it does converge, it might not be to a local optimum of the original problem, let alone a global optimum. The solution of successive iterations, and therefore subproblem inputs, can become wilder and wilder, until at some point …

[Amirhossein_Solati]

Hi,

I have been trying to code the objective and constraints, but I am currently facing a “Failed” status. In the following, I will attempt to explain my code and the main problem. I would greatly appreciate your help, as I have been stuck on this for the past four days since my last message. Thank you very much for your time.
here is Main Optimization Problem:

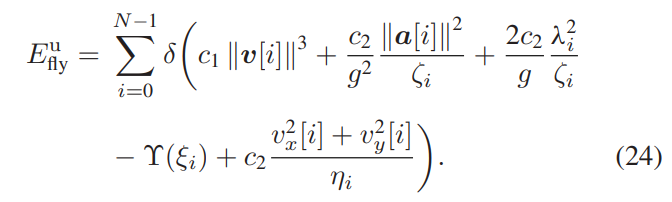
and here are Constraints and expressions:

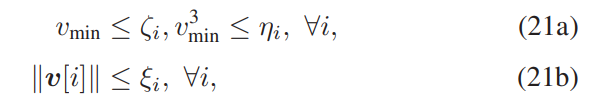
where Aux2 in my code is:

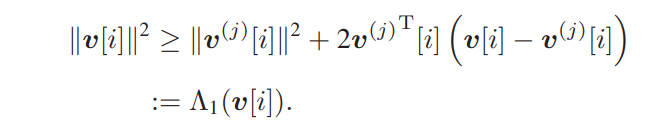
This is Optimization Problem kse, zeta and eta are Auxiliary variables. all parameters which declared with j index are local points( given points) As I did not get Solved Status I didn’t Iterate to get optimized point to use in next iteration I just Use randi(matlab Function) to generate local points.
Here is my code:

tic
warning off
clc
clear
close all
format short g
Define parameters and constants
c1   = 9.26e-4;
c2   = 2250;
kc   = 0.017;
alpha = 1334;
Emax = 20000;          % Maximum Battery Capacity in Joule
EI   = 2000;           % Initial Battery Capacity in Joule
Ef   = 2000;           % The Lowest Final Battery Energy in Joule
qI   = [1000;0;100]; % Initial Position Of UAV
qF   = [0;1000;100];             % UAV Return to its Initial Point
vI   = [25;25;25];      % UAV Initial Velocity
vF   = vI;             % UAV Final Velocity
vmin = 3;             % Minimum Speed Of UAV
vmax = 50;            % Maximum Speed Of UAV
amax = 5;             % Maximum Accelration
Hmin = 50;            % Minimum Alititude Of UAV
Hmax = 1800;          % Maximum Alititude Of UAV
teta = 15;            % Maximum Pitch Angle Of UAV
T    = 220;           % The Flight Duration Of UAV
delta = 0.1;          % Time Slot Duration
sigma = 10 ^ ((-90 - 30) / 10);     % Noise Power in watt
g0    = db2pow(-50);                % Refernce Channel Gain
B     = 10;                         % System Bandwidth
b1    = 20;                         % Probabilistic Channel Parameter
b2    = 0.15;           % ...
mu    = 0.1;            % ...
qk   = [150,350,0;      % Smart Devices Location
    400,120,0;
    50,100,0;
    450,450,0;
    250,0,0]';
% Round - Robin Channel Pameters
Pk    = 50;           % Transmission Power Of SD
% Los Channel Parameters
Pkmax = 100;          % UAV Transmission Power
Etotal = 2.2;         % Total Energy For SD in Joule
Initialize Parameters
N = 100;            % Duration Of Flight
K = 5;
tau = delta/K;
qx = randi([-500,2000],1,N+1);
qy = randi([-550,950],1,N+1);
qz = randi([50,1800],1,N+1);
vx = randi([80,100],1,N+1);
vy = randi([80,100],1,N+1);
vz = randi([80,100],1,N+1);
ax = randi([1,5],1,N+1);
ay = randi([1,5],1,N+1);
az = randi([2,4],1,N+1);
q0 = [qx;qy;qz];
a0 = [ax;ay;az];
v0 = [vx;vy;vz];
lan0 = az + amax;
kse0 = vecnorm(v0);
Ps0 = randi([50,550],1,N+1);
Variables Declare
cvx_clear
cvx_begin
variable q(3,N+1) % This is p which I Defined as q
variable v(3, N+1)
variable a(3, N+1)
variable kse(1,N+1)
variable zeta(1,N+1)
variable eta(1,N+1)
variable landa(1,N+1)
v0norm = vecnorm(v0);
Lower and Upper bounds
for n = 1:N+1
    Aux2(n) = 2*c2*0.10204*(amax/kse0(n) - amax*(kse(n) - kse0(n))/kse0(n)^2); % Upper Bound Od Kse eq.23
    Aux3(n) = v0norm(n)^2 + 2*v0(:,n)'*(v(:,n)-v0(:,n)); % Taylor Series for ||V||^2
    Aux4(n) = v0norm(n)^3 + 3*v0norm(n)*v0(:,n)'*(v(:,n)-v0(:,n)); % Taylor Series for ||V||^3
end
Objective Function
E = 0;
for n = 1:N
    efly = delta*(c1*pow_pos(norm(v(:,n)),3) + c2*0.0104*quad_over_lin(a(:,n),zeta(n)) ...
        + 2*c2*0.1*quad_over_lin(landa(n),zeta(n)) - Aux2(n) +c2*quad_over_lin(v(1,n),eta(n)) + c2*quad_over_lin(v(2,n),eta(n)));
    E = E + efly;
end
minimise(E)
subject to
q(:,1) == qI;      % C3
q(:,end) == qF;    % C3_1
v(:,1)==vI;        % C4
v(:,end)==vF;      % C4_1
q(:,2:end)  == q(:,1:end-1) + delta * v(:,1:end-1) + 0.125 * a(:,1:end-1); % C5
v(:,2:end) ==  v(:,1:end-1)  + delta * a(:,1:end-1); % C6
50 <= q(3,:); % C7
q(3,:) <= 500; %C7
for n = 1:N+1
    norm(a(:,n)) <= amax; % C8
    norm(v(:,n)) <= vmax; % C9
    vmin <= zeta(n); % C21a
    vmin^3 <= eta(n);% C21a
    norm(v(:,n)) <= kse(n) %C21b
end
a(3,:) + amax <= lan0.^2 + 2*lan0.*(landa - lan0); % C26
for n=1:N+1
    pow_abs(v(3,n),2) <= sin(deg2rad(teta)) * Aux3(n); % C28
    pow_p(zeta(n),2) <= Aux3(n) % C30
    eta(n) <= Aux4(n); %C31
end
cvx_end

and here is CVX Output:

 
Calling SDPT3 4.0: 5730 variables, 2206 equality constraints
   For improved efficiency, SDPT3 is solving the dual problem.
------------------------------------------------------------

 num. of constraints = 2206
 dim. of sdp    var  = 1404,   num. of sdp  blk  = 702
 dim. of socp   var  = 2112,   num. of socp blk  = 503
 dim. of linear var  = 1310
 dim. of free   var  = 202 *** convert ublk to lblk
*******************************************************************
   SDPT3: Infeasible path-following algorithms
*******************************************************************
 version  predcorr  gam  expon  scale_data
   HKM      1      0.000   1        0    
it pstep dstep pinfeas dinfeas  gap      prim-obj      dual-obj    cputime
-------------------------------------------------------------------
 0|0.000|0.000|1.8e+06|3.6e+01|8.1e+14|-6.175141e+12  0.000000e+00| 0:0:00| spchol  1  1 
 1|0.000|0.000|1.8e+06|3.6e+01|8.1e+14|-6.175140e+12 -2.172981e+06| 0:0:00| spchol  1  2 
 2|0.000|0.000|1.8e+06|3.6e+01|8.1e+14|-6.175135e+12 -1.370265e+07| 0:0:00| spchol  1  2 
 3|0.000|0.000|1.8e+06|3.6e+01|8.1e+14|-6.175130e+12 -3.586628e+07| 0:0:00| spchol  1  1 
 4|0.000|0.000|1.8e+06|3.6e+01|8.1e+14|-6.174936e+12 -1.380077e+08| 0:0:00|
 *** Too many tiny steps:  restarting with the following iterate.
 *** [X,y,Z] = infeaspt(blk,At,C,b,2,1e5); spchol  2  2 
 5|0.741|0.036|5.9e+06|9.8e-01|3.0e+13|-2.374843e+14 -2.651117e+08| 0:0:00| spchol  2  2 
 6|0.575|0.004|2.5e+06|9.8e-01|3.1e+15|-7.671823e+18 -3.220682e+08| 0:0:00| spchol  2  2 
 7|0.006|0.000|2.5e+06|9.8e-01|1.2e+19|-2.975510e+23 -1.295791e+09| 0:0:00| spchol * 3  3 
 8|0.000|0.000|2.5e+06|9.8e-01|5.8e+21|-1.716890e+26 -7.103767e+10| 0:0:00| spchol  1 * 3 
 9|0.000|0.000|2.5e+06|9.8e-01|3.6e+23|-1.056943e+28 -5.382841e+11| 0:0:00|
  sqlp stop: primal or dual is diverging, 1.1e+16
-------------------------------------------------------------------
 number of iterations   =  9
 Total CPU time (secs)  = 0.48  
 CPU time per iteration = 0.05  
 termination code       =  3
 DIMACS: 3.5e+07  0.0e+00  7.7e+00  0.0e+00  -1.0e+00  3.4e-05
-------------------------------------------------------------------
 
------------------------------------------------------------
Status: Failed
Optimal value (cvx_optval): NaN

I sincerely appreciate your assistance with my coding challenges. Thank you for taking the time to help me.

[Mark_L_Stone]

Perhaps you should re-read the link in my preceding post.

The solution of successive iterations, and therefore subproblem inputs, can become wilder and wilder, until at some point the solver fails, or makes erroneous determination of infeasibility or unboundedness.

You seem to have a misplaced expectation that a very unreliable algorithm (crude, unsafeguarded SCA) should be reliable.

[Amirhossein_Solati]

Can you share your suggestions on how to address this issue?
means that I should maybe try other solvers or maybe change the article?

[Mark_L_Stone]

It’s your research project, not mine. I am not your advisor. So I will leave determination of how to proceed to others.