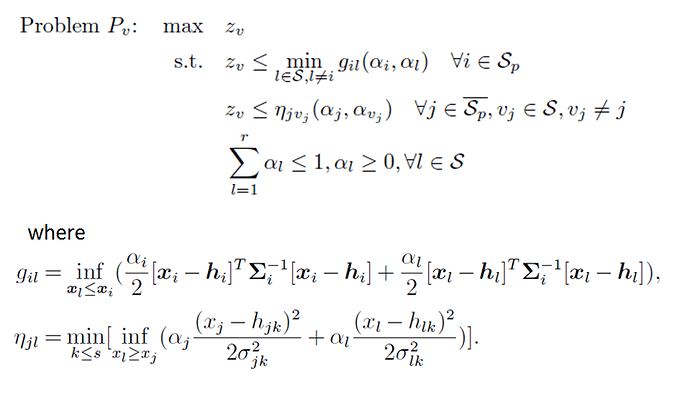Multi-level Convex Optimization and DCP Error (Cannot perform the operation: {real affine} .* {convex})

1

Dear all,

I’m trying to solve a nested/multi-level convex optimization problem as below.

Image 4.png806×464 65.2 KB

The decision variable includes z_v, alpha_1, …, alpha_r. (S = {1,2,…r}) The function g_il and eta_jv_{j} are concave functions with respect to corresponding alphas.

I defined incomplete specifications for the function g_il and eta_jv_{j} as following.

function cvx_optval = g_il(alpha_i,alpha_l,h_i,h_l,sigma_i_inv,sigma_l_inv)
[s,~] = size(h_i);
cvx_begin
variables x_i(s) x_l(s);
minimize(0.5alpha_iquad_form(x_i-h_i,sigma_i_inv) + 0.5alpha_lquad_form(x_l-h_l,sigma_l_inv));
subject to
x_l <= x_i;
cvx_end

function cvx_optval = min_g_il(alpha,i,h,sigma_inv)
[r,s]=size(h);
cvx_optval = 100000;
for l = 1:r
if l~=i
cvx_optval = min(cvx_optval,g_il(alpha(i),alpha(l),h(i,:)‘,h(l,:)’,sigma_inv{i},sigma_inv{l}));
end
end

function cvx_optval = eta_jl(alpha_j,alpha_l,h_j,h_l,sigma_j,sigma_l)
[s,~]=size(h_j);
cvx_optval = 100000;
for k = 1:s
cvx_begin
variables x_j x_l;
minimize(0.5alpha_j(x_j-h_j(k))^2/sigma_j(k)^2 + 0.5alpha_l(x_l-h_l(k))^2/sigma_l(k)^2);
subject to
x_l >= x_j;
cvx_end
cvx_optval = min(cvx_optval, 0.5alpha_j(x_j-h_j(k))^2/sigma_j(k)^2 + 0.5alpha_l(x_l-h_l(k))^2/sigma_l(k)^2);
end

In addition, the outer optimization problem (problem P_v) is as below

function cvx_optval = sub_cvx_prob(h,sigma,sigma_inv,v,nonPareto)
[r,s] = size(h);
cvx_begin
variable z;
variable p(r) nonnegative;
maximize(z);
subject to
for i = 1:r
if not(ismember(i,nonPareto))
z <= min_g_il(p,i,h,sigma_inv);
else
l = v(find(i==nonPareto));
z <= eta_jl(p(i),p(l),h(i,:)‘,h(l,:)’,sigma(i,:)‘,sigma(l,:)’);
end
end
sum(p) <= 1;
cvx_end

The problem is when I substitute numerical alpha into the g_il function, it works well. But when the problem is nested, then it raises the error

" Cannot perform the operation: {real affine} .* {convex}"

I found rare posts related to nested/embeded/multi-level convex optimization and the DCP rule sets seem a little tricky for me currently. Could anyone can help me figure out this problems? Please let me know if you want any further information. Thanks in advance.

Best,
Weizhi

2

Your larger problem simply is not convex in \alpha and x jointly.

Breaking it apart into nested functions doesn’t help, because CVX is always just solving one large expanded model. You will probably have to find a way to eliminate x analytically from your expressions of g_{il} and \eta_{jl} if you wish to use CVX.

Another thought I had was that if you could find the duals of your inner optimization problem, you might find that you get a problem that is convex jointly in \alpha and those dual variables.

3

Your problem reminds me of the following definition of CVX’s own sum_largest(x,k) function; this is a convex function that computes the sum of the largest k elements of x. A simple way to express this function in terms of an optimization model is
$$\begin{array}{ll}\text{maximize} _y& x^T y \ \text{subject to} & 0 \leq y \leq 1 \ & \sum_i y_i = k \end{array}$$
If you tried to build a CVX incomplete specification using this form, though, so that x can be a variable, it would fail, because of the x^T y product. And it should fail, because when CVX expands this out into a larger model, it is not jointly convex in x and y.

But CVX does have a sum_largest function; go take a look at it! Here is the model it uses instead:
$$\begin{array}{ll}\text{minimize}_{w,z} & -k w + \sum_i z_i \ \text{subject to} & z \geq w \vec{1} + x \ & z \geq 0 \end{array}$$
the variables here are a scalar w and z\in\mathbb{R}^n. This is a form of the dual of the model above, and you’ll note that now there are no products between the variables. So when CVX expands this out, the problem is jointly convex in x, w, and z.

This is the kind of manipulation I think you’ll want to try and accomplish with your problem, if you cannot eliminate the x values completely.

4

Hi mcg,

Thanks for your prompt reply and rich experience. I do believe the two approaches you provided are promising to solve my problems.

  1. The inner optimization of g_{il} and \eta_{jl} are just constrained quadratic programming which should be easy to derive the analytical solutions by KKT condition.
  2. Adopting the dual problem to avoid the DCP product error of incomplete specification is quite brilliant. Thanks for your suggestions and I might use this idea for the future implementation of CVX.

Besides, I have something to clarify about the mechanism of CVX.

  1. As you mentioned, CVX is always just solving one large expanded model. Does that mean when CVX solve the inner optimization, the exogeneous variables are still symbolic (or say affine/constant/convex/concave expression) instead of numerical values? Therefore, the larger optimization problem should be jointly convex in all the variables?
  2. I remember some guys said that the incomplete specification should be affine with respect to the parameterized variable. But in the dual formulation of sum_largest(x,k) function, the parameterized variable x is in the constraint, how can we say this incomplete specification is affine w.r.t x?

The reason I choose CVX is because actually the fmincon() function in matlab doesn’t seem to converge to the global optimum for convex optimization problem (use the interior-point algorithm). I have a larger problem P which is not convex and I decompose it into several P_{v} which is convex. By combining the results, I can find the global optimum of original problem P. Therefore, I compared the procedure of solving problem P directly and solving sub-problems P_{v} based on fmincon(). But it gives me the same results, maybe the fmincon() has already gave me the global optimum but I’m not sure. Therefore, I want to implement CVX to see if the performance can be improved.

I really appreciate your suggestions and thanks for your kind help.

Thanks,
Weizhi

5

Think about incomplete specifications like macros. The inner optimization is never solved separately; it is merged into the larger problem. So yes, the exogenous variables remain symbolic. Thus the model must obey the DCP rules with respect to all variables.

6

Got it and thank you very much. Have a great day!

Thanks,
Weizhi

8

Hi mcg,

The dual problem of g_{il} is as below,

\begin{equation}
\begin{aligned}
\mbox{maximize} \quad & -\frac{1}{2} \lambda^{T} [\frac{\Sigma_{i}}{\alpha_{i}} + \frac{\Sigma_{l}}{\alpha_{l}}]\lambda + \lambda^{T}[h_{l}-h_{i}] \
\mbox{s.t.} \quad & \lambda \succeq 0 \
\end{aligned}
\end{equation}

Could it be possible to solve it via CVX given \alpha_{i}, \alpha_{l} are exogenous parameter of outer optimization?

Based on the P142 of Convex Optimization, the optimality condition of this dual problem is as below
\begin{equation}
\begin{aligned}
\lambda & \succeq 0 \
[\frac{\Sigma_{i}}{\alpha_{i}} + \frac{\Sigma_{l}}{\alpha_{l}}]\lambda + h_{i} - h_{l} & \succeq 0 \
\lambda^{T} [\frac{\Sigma_{i}}{\alpha_{i}} + \frac{\Sigma_{l}}{\alpha_{l}}]\lambda + \lambda^{T}[h_{i}-h_{l}] & = 0\
\end{aligned}
\end{equation}

May I ask if the condition above could be solved analytically? Thanks for your kind help. :smile:

Can I conclude that \lambda^{*} = \max( [\frac{\Sigma_{i}}{\alpha_{i}} + \frac{\Sigma_{l}}{\alpha_{l}}]^{-1}(h_{l}-h_{i}), 0) for the constrained quadratic optimization? Because this solution can let either first two inequalities in optimality condition binding which means the complementary slackness is satisfied.

Last question is that can we formulate harmonic mean function which is concave based on the DCP ruleset? I tried several ways, but all of them conflict with composition rule… Since my \eta_{jl} is represented by the following expression

\begin{align*}
\eta_{jl}
& = \mathbb{I}{(l \prec j)} \cdot \min\limits{k \le s} \frac{(h_{jk}-h_{lk})^2}{ 2( \sigma_{{jk}}^2/\alpha_j + \sigma_{{lk}}^2/\alpha_l ) } .
\end{align*}

which is composed by the harmonic mean function.

Thanks,
Weizhi