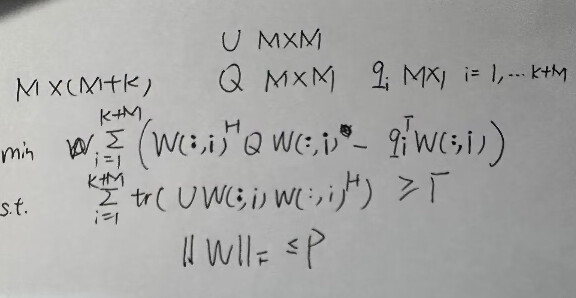
I have this question that i plan to use SDP to solve it, i plan to set a auxiliary variables vector s (M+K*1) and new w_i=[W(:,i) ; s(i)]. Generally, we introduce an s and i dont know if it is solvable for a group of s.
I don’t know what your plan is.
I will presume the W just to the right of min denotes minimize w.r.t W
If Q is hermitian semidefinite and U is negative hermitian semidefinite (i.e., -U is hermitian semidefimnite), the problem appears to be convex and enterable into CVX. Otherwise, not convex.
Presuming U is negative hermitian semidefinite, and using the cyclic permutation invariance of trace, the summand of the first constraint can be reformulated as -square_pos(norm(sqrtm(-U)*W(:,i),'fro')). So this constraint won’t make much sense unless the RHS is negative (non-positive). On the other hand, if U were hermitian semidefinite, the constraint would make sense with a positive RHS, but would be non-convex.