Dear ALL,
I have tried to solve the following convex optimization problem with binary decision variables:
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clc;
N = 3;
L = 5;
beta = 0.5;
alpha = 4;
phi = ones(L, 1);
mu = ones(N, 1);
M = ones(N, 1);
eta = L/sum(M);
dist = zeros(L, L);
position = zeros(L,1);
for i = 1:L
position(i, 1) = 1000rand();
position(i, 2) = 1000rand();
end
for i = 1:L
x1 = position(i, 1);
y1 = position(i, 2);
for j = 1:L
x2 = position(j, 1);
y2 = position(j, 2);
dist(i,j) = sqrt((x1-x2)^2 + (y2-y1)^2);
dist(i,j) = dist(i,j)^2;
end
end
P = zeros(N, L);
for i = 1:N
for j = 1:L
P(i,j) = min(1, mu(i)/phi(j));
end
end
cvx_begin
variable y(L,L,N) binary %%%% ylki = xil*xik auxiliary variable for linearlizing product of two variable x
variable x(N, L) binary %%% binary variable for cell assignment
for i = 1:N
F(i) = - x(i,:)*P(i,:)’ - (1/M(i))*x(i,:)*phi;
for l = 1:L
F(i) = F(i) + y(l,:,i)*dist(i,:)’; %%
end
end
%%% the primary objective is min max(F(i))
%%%% convert minmax to a convex problem as sum(Fi^alpha)/(alpha - 1)
fun = F(1)^alpha;
for i = 1:N
fun = fun + F(i)^alpha;
end
fun = fun/(alpha - 1);
cvx_solver MOSEK
minimize(fun);
subject to
for l = 1:L
sum(x(:, l)) == 1
end
for i = 1:N
for l = 1:L
for k = 1:L
y(l,k,i) <= x(i, l)
y(l,k,i) <= x(i, k)
y(l,k,i) >= x(i, l) + x(i, k) - 1
end
end
end
cvx_end
x
y
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
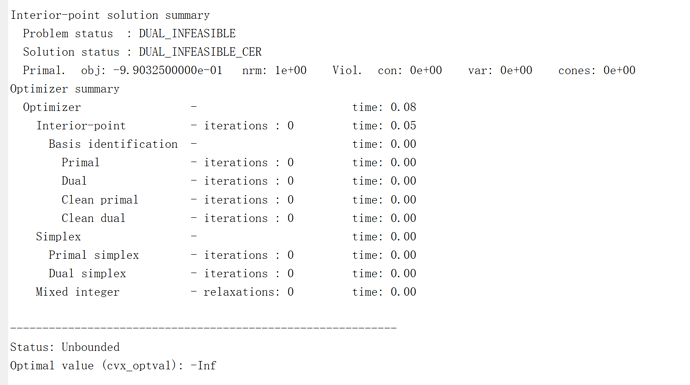
The output is
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Calling Mosek 8.0.0.60: 341 variables, 98 equality constraints
For improved efficiency, Mosek is solving the dual problem.
MOSEK Version 8.0.0.60 (Build date: 2017-3-1 13:09:33)
Copyright © MOSEK ApS, Denmark. WWW: mosek.com
Platform: Windows/64-X86
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 98
Cones : 8
Scalar variables : 341
Matrix variables : 0
Integer variables : 90
Optimizer started.
Mixed integer optimizer started.
Threads used: 2
Presolve started.
Presolve terminated. Time = 0.00
Presolved problem: 323 variables, 91 constraints, 693 non-zeros
Presolved problem: 0 general integer, 90 binary, 233 continuous
Clique table size: 0
BRANCHES RELAXS ACT_NDS DEPTH BEST_INT_OBJ BEST_RELAX_OBJ REL_GAP(%) TIME
0 1 0 0 NA -2.1609629032e-007 NA 0.1
0 1 0 0 0.0000000000e+000 -2.1609629032e-007 2.16e+005 0.1
0 1 0 0 -4.3419370574e-008 -2.1609629032e-007 397.70 0.1
Cut generation started.
0 2 0 0 -4.3419370574e-008 -2.1609629032e-007 397.70 0.2
Cut generation terminated. Time = 0.00
3 6 0 1 -6.0944914982e-007 -6.0944914982e-007 0.00e+000 0.2
An optimal solution satisfying the relative gap tolerance of 1.00e-002(%) has been located.
The relative gap is 0.00e+000(%).
An optimal solution satisfying the absolute gap tolerance of 0.00e+000 has been located.
The absolute gap is 0.00e+000.
Objective of best integer solution : -6.094491498218e-007
Best objective bound : -2.160962903238e-007
Construct solution objective : Not employed
Construct solution # roundings : 0
User objective cut value : 0
Number of cuts generated : 0
Number of branches : 3
Number of relaxations solved : 6
Number of interior point iterations: 81
Number of simplex iterations : 0
Time spend presolving the root : 0.00
Time spend in the heuristic : 0.00
Time spend in the sub optimizers : 0.00
Time spend optimizing the root : 0.02
Mixed integer optimizer terminated. Time: 0.23
Optimizer terminated. Time: 0.30
Integer solution solution summary
Problem status : PRIMAL_FEASIBLE
Solution status : INTEGER_OPTIMAL
Primal. obj: -6.0944914982e-007 nrm: 3e-001 Viol. con: 8e-009 var: 6e-008 cones: 0e+000 itg: 4e-008
Optimizer summary
Optimizer - time: 0.30
Interior-point - iterations : 0 time: 0.00
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 6 time: 0.23
Status: Solved
Optimal value (cvx_optval): NaN
x =
NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN
y(:,:,1) =
NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN
y(:,:,2) =
NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN
y(:,:,3) =
NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN
NaN NaN NaN NaN NaN
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
In my primary problem, the objective function F(i) includes the problem of two binary variables xilxk. So, I linearize it by adding auxiliary variable ylki = xilxik with additional constrains as
ylki <= xil
ylki = xik
ylki = xil + xik -1
However, I do not know why the program returns NaN for objective function and all binary variables x,y.
I am new with CVX. Please help me to chech this problem.
Thanks.