Modeling scalene(x,2,-3) as quasilinear function

1

Hello,

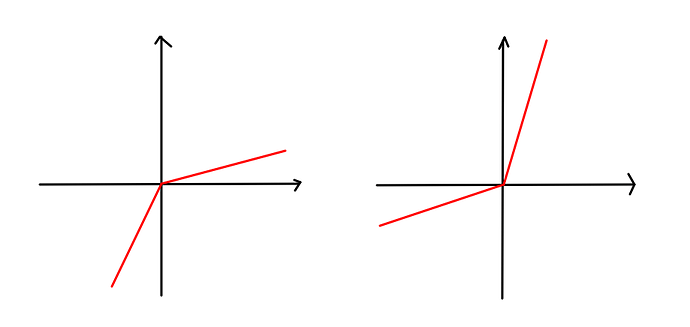
scalene(x,a,b) is abbreviation for a*pos(x)+b*neg(x) for positive a and b (documentation).

For my purposes, I need b to be negative. This leads to quasi-linear functions of these shapes:

quasilinear
quasilinear919×436 9.26 KB

My problem is that CVX do not recognize quasi-linearity and it report UNKNOWN curvature.

How can I model scalene(x,2,-3) as function of QUASILINEAR curvature in CVX?

To be specific, in the end I need constraints

[sum(scalene(v[i]-v[j],S[i,j],-S[j,i])) for i in [1…n])==0] for j in [1…n]]`

where S[i,j] are some positive constants.

2

Read section 4,2,5 “Quasiconvex optimization” of https://web.stanford.edu/~boyd/cvxbook/bv_cvxbook.pdf , and in particular, see the bisection algorithm,.

Alternatively, you can use CVXPY’s Disciplined Quasiconvex Programming https://www.cvxpy.org/tutorial/dqcp/index.html which will implement the bisection for you.

3

Hello, thank you for reply. I read both proposed sources very carefully, but I have not found answer to my problem. I know how does the Quasi-linear convex optimalization work. My problem is that CVX does not recognize my special function to be quasi-linear.

4

Mark says you should use cvxpy instead of cvx if you want to do quasiconvex optimization. In other words you cannot use cvx for your problem.

5

Ahh, I see. I am using CVXPY. And it reports UNKNOWN curvature od my quasilinear function, so I cannot run a solver, even if using qcp=True parameter.

6

I would ask at cvxpy on stackexchange