I am new to CVX and I am working on understanding the Users’ Guide. I do have a problem that I am trying to minimize an expression made by following requirement:

So I take Pg,m and sigma^2 as variables and p^og,m as the expression to achieve this optimization problem. I am pretty sure this problem is a CVX problem.
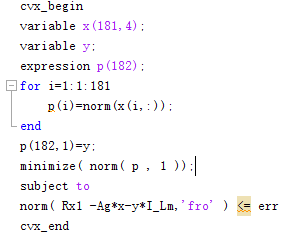
I did the above attempt but results are as follows:

I have been working on this problem for nearly a week but I cannot sort it out.
If possible, can someone tell me where am I wrong 
norm(p,1) is a norm of a norm, which is not allowed in CVX, because the argument of norm must be affine,
help cvx/norm
Disciplined convex programming information: norm is convex, except when P<1, so an error will result if these non-convex "norms" are used within CVX expressions. norm is nonmonotonic, so its input must be affine.
I believe norm(p,1) can be reformulated as sum(p). Actually, the for loop for p(i) and norm(p,1) can be replaced by sum(norms(x,[],2))
help norms
norms Computation of multiple vector norms.
norms( X ) provides a means to compute the norms of multiple vectors
packed into a matrix or N-D array. This is useful for performing
max-of-norms or sum-of-norms calculations.All of the vector norms, including the false "-inf" norm, supported by NORM() have been implemented in the norms() command. norms(X,P) = sum(abs(X).^P).^(1/P) norms(X) = norms(X,2). norms(X,inf) = max(abs(X)). norms(X,-inf) = min(abs(X)). If X is a vector, these computations are completely identical to their NORM equivalents. If X is a matrix, a row vector is returned of the norms of each column of X. If X is an N-D matrix, the norms are computed along the first non-singleton dimension. norms( X, [], DIM ) or norms( X, 2, DIM ) computes Euclidean norms along the dimension DIM. norms( X, P, DIM ) computes its norms along the dimension DIM. Disciplined convex programming information: norms is convex, except when P<1, so an error will result if these non-convex "norms" are used within CVX expressions. norms is nonmonotonic, so its input must be affine.
Thanks Mark,
I do really learn a lot from your suggestion which helps me sort out more optimization problems.