Hi,
I am trying to detect communities using binary min cut on users’ graph. For this purpose I am trying to use a variant of Fiedler method as shown in this paper. This is how they have formalized it:
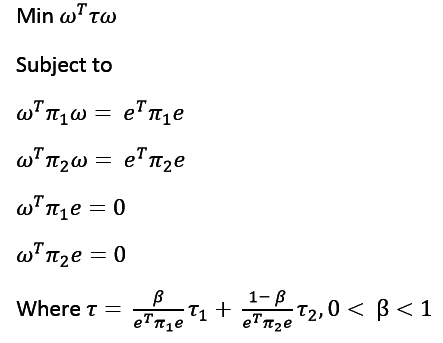
Now, I am trying to do this using the CVX package in matlab. Here is my code:
tou = ((beta/ (e' * pi1 * e)) * tou1) + (((1 - beta) / (e' * pi2 * e)) * tou2);
n = 6;
cvx_begin
variable y(n)
minimize( y' * tou * y )
subject to
y' * pi1 * y == e' * pi1 * e
y' * pi2 * y == e' * pi2 * e
y' * pi1 * e == 0
y' * pi2 * e == 0
cvx_end
But it is showing me the following error:
Disciplined convex programming error:
Invalid constraint: {convex} == {real constant}
Error in ==> cvx.eq at 12
b = newcnstr( evalin( 'caller', 'cvx_problem', '[]' ), x, y, '==' );
Error in ==> fiedler at 16
y' * pi1 * y == e' * pi1 * e
Here A1 is a matrix defined as follows:
A1 = [0 3 2 0 0 0; 3 0 3 1 0 0; 2 3 0 0 0 0; 0 1 0 0 4 2; 0 0 0 4 0 3; 0 0 0 2 3 0];
Similarly A2 = A1.
And pi1 is a matrix is a diagonal matrix whose value is equal to sum of all the values of A1 in that particular row. Doing so I get
pi1 = [5 0 0 0 0 0; 0 7 0 0 0 0; 0 0 5 0 0 0; 0 0 0 7 0 0; 0 0 0 0 7 0; 0 0 0 0 0 5];
Similary, pi1 = pi2.
And tou1 = pi1 - A1, and tou2 = pi2 - A2.
Can someone point out what exactly I am doing wrong. It would be of great help. Thanks in advance !