Hello.
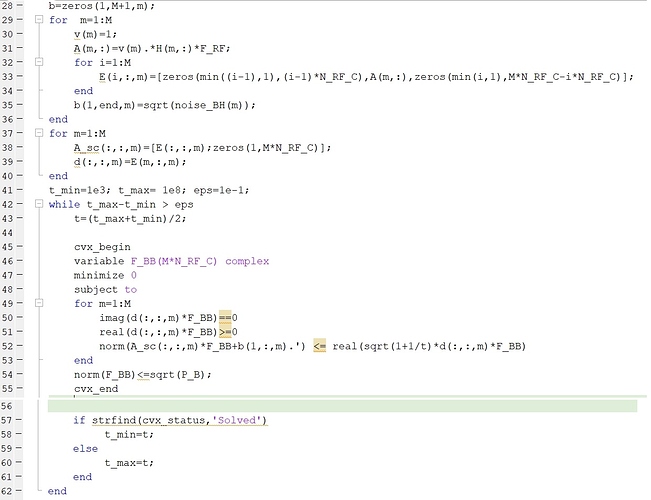
I have written the following codes to implement problem in CVX.
I have used the bisection algorithm to solve it.
After that, CVX says “Solved,” but I found some constraints have been violated when I check the (50,51,52) constraints. So the algorithms don’t work well, and the answer is wrong.
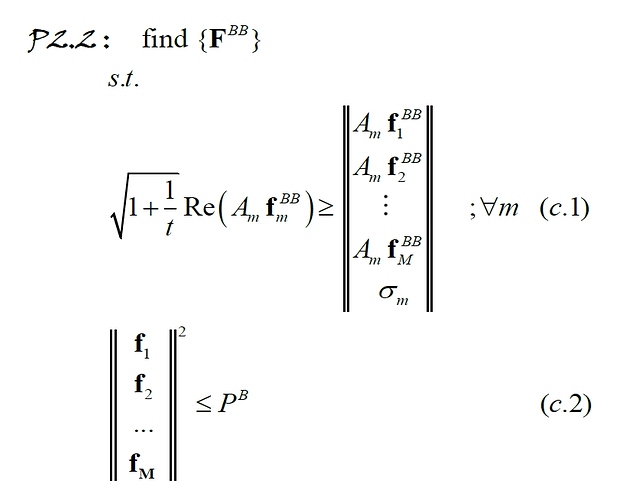
It is important to know I want the imaginary part of (A_m * F_m) to be zero as well as its real part is a nonnegative variable.
Actually, I have to use Real in constraint (c.1), because Matlab says “Invalid constraint: {convex} <= {complex affine}” when I don’t
1 Like
H , F_RF are predefined matrices. As well as P_B, noise_BH.
1 Like
When the solver and CVX claim a problem is solved, constraints may still be violated by up to a solver tolerance. Show us the solver and CVX output, and the amount by which the constrains are violated.
And in the future, post your code using Preformatted text icon, rather than posting an image.
1 Like
Thanks for replying and for your good advice.
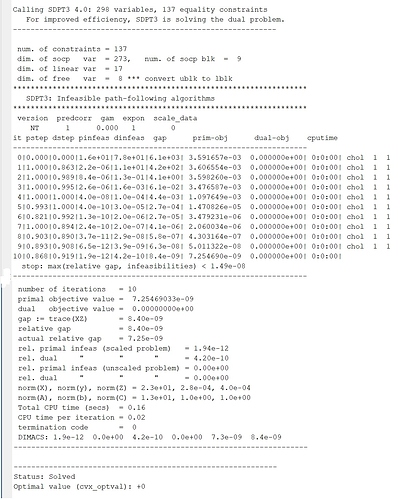
As you can see in the following picture, I test the constraint (52), and the answer is “0”.
Actually, my main problem is that I set the “t_max” in a very large value, for example, 1e30, but always the algorithm rich this point and say the problem “Solved.”
CVX output in the last iteration …
1 Like
Setting t_max to a value such as 1e30 may cause difficulties in the solver. Anything larger than 1e4 or 1e5 may not be good. if you set it to such a smaller value and it it reached in a solution, you may need to reexamine your model.
You tested for exact satisfaction of the constraint. However, the solver may violate it by up to a constraint tolerance, such as 1e-8.
Edit: You say the t_max value of 1e30 is reached. So perhaps your model , to include all input data, needs rethinking or improvement
Edit2: O.k., now i see this has something to do with your bisection algorithm. Do you have the initial bracketing done properly?
1 Like