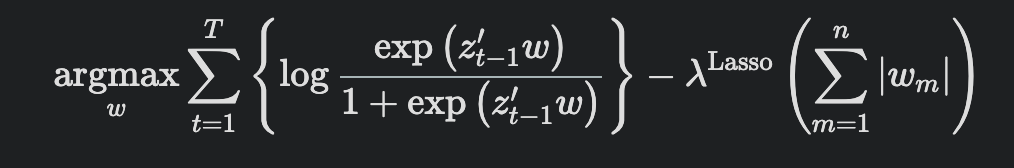The following expression arises in the objective function for logistic regression and I was told the function is convex:
log(1 / (1+exp(-z)).
Is it possible to write this function in a way that CVX will recognize its convexity?
log(1/(1+exp(-z))) is actually concave, and CVX recognizes and accepts it as such, so for instance, you can maximize it as an objective function in CVX. It will require use of CVX’s successive approximation method (which will be invoked automatically), as described in the CVX user’s guide. Of course, log(1+exp(-z)) being -log(1/(1+exp(-z))) is convex and can be minimized, which will accomplish the same thing.
See http://cvxr.com/cvx/examples/cvxbook/Ch07_statistical_estim/html/logistics.html for an example of logistic regression performed in CVX, and also http://matlab-code-by-wayne.googlecode.com/svn/branches/cvx/examples/cvxbook/Ch07_statistical_estim/html/logistics_gp.html , which additionally shows reformulation of logistic regression as a Geometric Program and solution in CVX by use of CVX’s Geometric Programming mode, which, as stated in the CVX user’s guide, also uses CVX’s successive approximation method.
It might be a bit surprising to CVX power users that log(1/(1+exp(-z))) is accepted by CVX. After all, it does not seem to obey the disciplined convex programming ruleset!
But in fact, in order to support geometric programming, CVX has a lesser known set of rules governing log convexity as well. The definition of log convexity is this: if a function is positive and its logarithm is convex, then it is log-convex. There are equivalent definitions of log-affine and log-concave functions as well.
We don’t publish the log-convexity rules explicitly. But if you’re a power user you might be interested in them. First, we have the following rules that take you back and forth between the “standard” convexity world and the log-convexity world:
-
exp(*affine*)is log-affine;exp(*convex*)is log-convex;exp(*concave*)is log-concave. -
log(*log-affine*)is affine;log(*log-convex*)is convex;log(*log-concave*)is concave. - Log-affine expressions are also log-concave and log-convex.
- Positive constants are log-affine, log-concave, and log-convex.
Given those basics, you can actually take most of the basic DCP rules and map them to log-convexity:
- Products: products of {log-affine,log-convex,log-concave} expressions are {log-affine,log-convex,log-concave}. This is the log-convexity equivalent of DCP’s sum rules.
- Positive exponents: A {log-affine,log-convex,log-concave} expression raised to a positive constant power is {log-affine,log-convex,log-concave}. This is the log-convexity equivalent of DCP’s positive scaling rules.
- Negative exponents: A {log-affine,log-convex,log-concave} expression raised to a negative constant power is {log-affine,log-concave,log-convex}. This is the log-convexity equivalent of DCP’s negative scaling rules.
- Ratios: The ratio of a {log-convex,log-concave,log-affine} and a {log-concave,log-convex,log-affine} expression is {log-convex,log-concave,log-affine}. This is the equivalent of differences in DCP. So, not surprisingly, taking the ratio of two log-convex expressions is invalid, because this would be equivalent to subtracting one convex expression from another.
There is one rule for log-convexity, however, that does not have a DCP analog. It is this:
- Sums of log-affine and/or log-convex expressions are log-convex. Sums of log-concave expressions are not permitted. Note that even if every term of the sum is log-affine, the resulting sum is log-convex.
Confusing? Well, yeah, it is. But let’s go through log(1/(1+exp(-z))) to see why CVX accepts it:
- Both
1andexp(-z)are log-affine. - The sum
1+exp(-z)is therefore log-convex. - The ratio
1/(1+exp(-z))is log-concave. Alternatively, it is equivalent to(1+exp(-z))^(-1), which is log-concave by the negative exponent rule. - Therefore,
log(1/(1+exp(-z)))is concave.
Suggestion to mcg: Please add the CVX log-convexity and log-concavity rules to the next version of the CVX user’s guide. Thanks.
Frankly this is the first time I’ve written them all out! They kind of fell out by accident when I was implementing the geometric programming support. I probably should include them, in at least an advanced section.
My one hesitation is that it still relies on the successive approximation system. I really don’t want to encourage its use any more than necessary  But in fact, GPs seem reasonably reliable compared to log/exp in general, so maybe this will be kind of harmless.
But in fact, GPs seem reasonably reliable compared to log/exp in general, so maybe this will be kind of harmless.
Mark, I have indeed added a section to the advanced chapter of the CVX manual. It will come out with the next major release (we’ve got a new capability coming so it’s a semi-major release, not my normal rapid release style).
my objective function minimize -(Mn - mu_n (1+exp(convex))
where mu_n is non-negative parameter
Mn is constant value
error is real (affine.*log convex)
How to solve this
Per my answer to you at If dual variables are non negative, Is there need to initialized?
If mu_n does not appear in any constraints other than being nonnegative, mu_n = 0 is optimal, together with any feasible values of the other variables.
Thank you, Sir
Can i formulate lagrangian dual function like this
cvx_begin quiet
cvx_solver mosek
variable Pi %optimization variables
variable Pj
dual variables nu rho eta phi
minimize -(Mn-mu_n.*(1+exp(-an.*(gnx(1,i).*(Pi+Pj)-bn)))+nu.*(Pi.*hix(1,1)-Omega_i.* (Pj.*hix(1,1)+Ni))+ rho.*(Pj.*hjx(1,1)-Omega_j.*Nj)+ eta.*(Pi.*hjx(1,1)-Omega_t.*(Pj.*hjx(1,1)+Nj))+sum(phi.*(Gamma_m-qmx.*(Pi+Pj)))) % optimizing Pi and Pj (optimal allocated power)
subject to
nu >= 0;
rho >= 0;
eta >= 0;
phi >= 0;
mu_n >= 0;
cvx_end
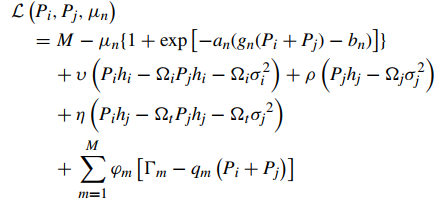
Warning like this,
Warning: A non-empty cvx problem already exists in this scope.
It is being overwritten.
In cvxprob.cvxprob at 28
In cvx_begin at 41
In feb19 at 43
Error using evalin
Undefined function ‘times’ for input arguments of type ‘cvxdual’.
Error in minimize (line 14)
x = evalin( ‘caller’, sprintf( '%s ', varargin{:} ) );
Error in feb19 (line 48)
minimize -(Mn-mu_n.(1+exp(-an.(gnx(1,i).(Pi+Pj)-bn)))+nu.(Pi.hix(1,1)-Omega_i.(Pj.hix(1,1)+Ni))+ rho.(Pj.hjx(1,1)-Omega_j.Nj)+
eta.(Pi.hjx(1,1)-Omega_t.(Pj.hjx(1,1)+Nj))+sum(phi.(Gamma_m-qmx.(Pi+Pj)))) % optimizing Pi and Pj (optimal allocated power)
You will not find anywhere in the CVX Users’ Guide which allows you to use declared dual variables in any manner other than as described at http://cvxr.com/cvx/doc/basics.html#dual-variables . Hence the error message. Declared dual variables can be associated with constraints as described in that section, and their values will be populated by CVX after it completes, but that is their only usage. i
f you want to do something more with a variable, it needs to be declared as a (CVX) variable, not as a dual variable. And of course CVX’s DCP rules must be followed.
Thank you for all the information provided in this post.
Would the a sum of log(1/(1+exp(-z))) be consistent with the geometric programming principle and accepted by CVX?
More specifically I am interested in solving a problem with the following formulation:
Can it be translated into CVX?
Yes. the summand reduces to
z(t-1)'*w -log(1+exp(z(t-1)'*w)) = z(t-1)'*w -log_sum_exp([0 z(t-1)'*w]), the latter of which will be accepted by CVX, and can be vectorized over the terms in the summand, as seen in the previously linked http://cvxr.com/cvx/examples/cvxbook/Ch07_statistical_estim/html/logistics.html . You can use the 1-norm for the Lasso “penalty” term.
There is no need to invoke GP mode for this problem.
Thank you, that’s really helpful. For the summation (1 to T), do you recommend using a loop as suggested in other posts and then adding the penalty term?
You can do that. But if the model is big, for loops for processing CVX expressions or constraints cam be slow. The CVX formulation time will be faster if you use sum on a vectorized argument, similar to
maximize(y'*U*x-sum(log_sum_exp([zeros(1,m); x'*U']))) as in the link in my previous post (change the variables accordingly for your problem) and add the lasso penalty term.
This explains how to input the arguments the right way. All the mentions of log_sum_exp_sdp also apply to log_sum_exp; it looks like the help text got conflated between the two related functions.
help log_sum_exp
log_sum_exp log(sum(exp(x))).
log_sum_exp(X) = LOG(SUM(EXP(X)).When used in a CVX model, log_sum_exp(X) causes CVX's successive approximation method to be invoked, producing results exact to within the tolerance of the solver. This is in contrast to LOGSUMEXP_SDP, which uses a single SDP-representable global approximation. If X is a matrix, LOGSUMEXP_SDP(X) will perform its computations along each column of X. If X is an N-D array, LOGSUMEXP_SDP(X) will perform its computations along the first dimension of size other than 1. LOGSUMEXP_SDP(X,DIM) will perform its computations along dimension DIM. Disciplined convex programming information: log_sum_exp(X) is convex and nondecreasing in X; therefore, X must be convex (or affine).