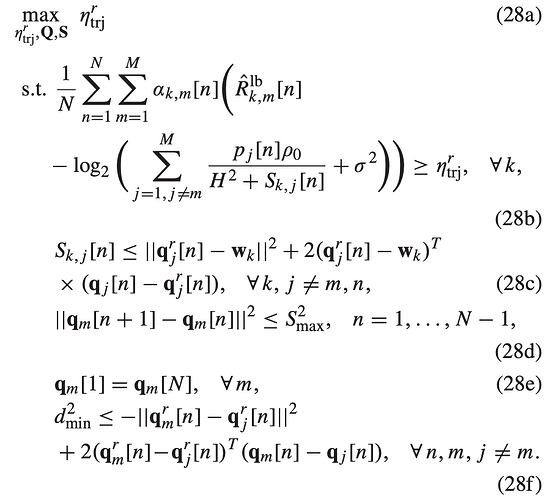Log{convex error}

1

Hi,
I want to maximize the objective function -log(P_max* rho_0 (inv_pos(H^2 + S(n,m))) + sigma_squ)
which is subject to : 0<=S(n,m) <=pow_pos(norm(Q(n,: ) - w(m,: )), 2) + 2(Q(n,: ) - w(m,:))*transpose(Q_2(n,: ) - Q(n,: ));
In this expression where Q_2(n,m) is a variable matrix
but I get log(convex) error from the objective function, is there any other way to rewrite these expression to avoid this CVX log(convex) constraint? The whole code is as follows:
cvx_begin
variable Q_2(N+1,2)
variable Q_2_other(N+1,2)
variable S(N,K)
variable S_other(N,K)
variable t(N,K)
variable t_other(N,K)
rate_sum_2 = 0.0;
for n=1:N
for m=1:K
dist_sq_Q = norm(Q(n,: ) - w(m,: ))^2;
dist_sq_Q_other = norm(Q_other(n,: ) - w(m,: ))^2;
B_raw = P(n)*rho_0/(dist_sq_Q + H^2) + P_other(n)*rho_0/(dist_sq_Q_other + H^2) + sigma_squ;

            A =       P(n)      *rho_0/((dist_sq_Q     + H^2)^2).*log2(exp(1))/B_raw;
            A_other = P_other(n)*rho_0/((dist_sq_Q_other + H^2)^2).*log2(exp(1))/B_raw;
            B=log2(B_raw);
            norm_x = norm(Q_2(n,: ) - w(m,: ));
            norm_x_other = norm(Q_2_other(n,:) - w(m,: ));
            
            mult_x = pow_pos(norm_x,2) - dist_sq_Q;
            mult_y = pow_pos(norm_x_other,2) - dist_sq_Q_other;

            R_lb = -A * mult_x - A_other * mult_y + 2*B;
            log_denom      = log(P(n)        * rho_0 *(inv_pos(H^2 + S(n,m)))      + sigma_squ)/log(2);
            log_denom_other= log(P_other(n)  * rho_0 *(inv_pos(H^2 + S_other(n,m)))+ sigma_squ)/log(2);
            
            rate_sum_2 =rate_sum_2 + alpha_switch(n,m) * (R_lb - log_denom_other) + alpha_switch_other(n,m) * (R_lb - log_denom);
        end
    end
    maximize(rate_sum_2)
    subject to 
    
    for n=1:N
        pow_pos(norm(Q_2(n+1,: ) - Q_2(n,: )), 2) <= (S_max^2);
        pow_pos(norm(Q_2_other(n+1,: ) - Q_2_other(n,: )), 2) <= (S_max^2);
        d_min^2 <= pow_pos(norm(Q(n,: ) - Q_other(n,: )), 2) + 2*(Q_other(n,: ) - Q(n,: )) * transpose(Q_2_other(n,: ) - Q_2(n,: ));
        for m=1:K
            0<=S(n,m)      <=pow_pos(norm(Q(n,: )       - w(m,: )), 2) + 2*(Q(n,: )       - w(m,:))*transpose(Q_2(n,: ) - Q(n,: ));
            0<=S_other(n,m)<=pow_pos(norm(Q_other(n,: ) - w(m,: )), 2) + 2*(Q_other(n,: ) - w(m,:))*transpose(Q_2_other(n,: ) - Q_other(n,: ));
            %t(n,m)       >= P(n)        * rho_0 *(inv_pos(H^2 + S(n,m)))      + sigma_squ;
            %t_other(n,m) >= P_other(n)  * rho_0 *(inv_pos(H^2 + S_other(n,m)))+ sigma_squ;
        end
    end 
    Q_2(N+1,: ) == Q_2(1,: );
    Q_2_other(N+1,: ) == Q_2_other(1,: );
cvx_end
2

Have you proven that this is a convex optimization problem? That is your first step.

3

I got this from a paper: Equation 28(b)

Screenshot 2025-06-06 at 15.08.05
Screenshot 2025-06-06 at 15.08.05914×817 68.5 KB

https://scholar.google.com/scholar?hl=en&as_sdt=0%2C5&q=Joint+Trajectory+and+Communication+Design+for+Multi-UAV+Enabled+Wireless+Networks&btnG=

4

In the paper, it is said that, the convexity is done by introducing a slack variable called (S_{k,j}[n]

5

By the way, I plotted the result of log2(…) function and it is really convex except at S_{k,j}[n]=-H^2 point.

6

I think the log term in (28b) can be handled using log-sum-inv Search results for 'log-sum-inv' - CVX Forum: a community-driven support forum . You’ll need to first convert the log2 into log by dividing it by log(2); then you can apply log-sum-inv to the log.

In any event, you should strive to understand exactly what everything in that formulation is, and why it does what it is needed. Superficial “hand waving” understanding of it is likely to lead to failure to correctly implement it.