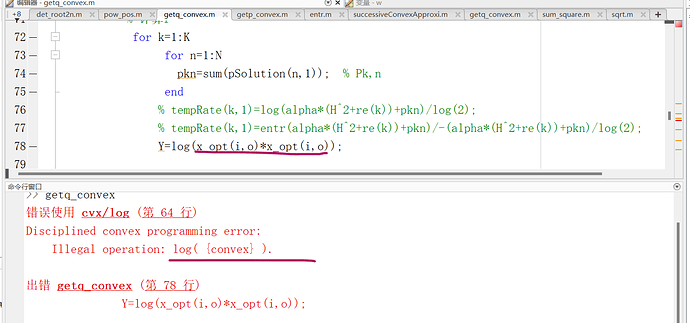
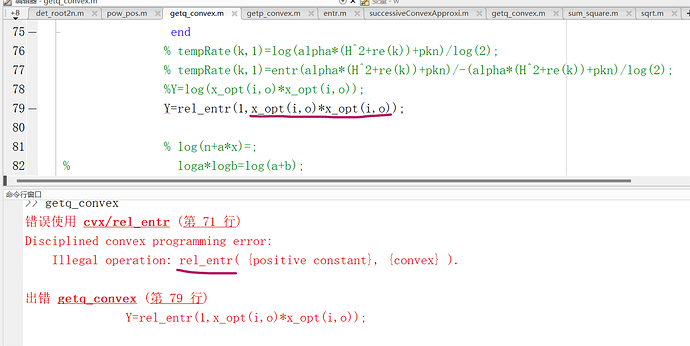
Why I cannot use {convex}{convex} in the log function ? I tried three forms: log(x_optx_opt) ; log(pow_pos(x_opt,2) ) ; log(x_opt.^2 ) . But they are all wrong.
log(x_opt(i,o)*x_opt(i,o)) = 2*log(x_opt(i,o)) . The LJS doesn’t obey CVX’s rules. The RHS does.
Sorry! I didn’t express clearly. I meet a problem about log(a+bx opt.^2). We can’t convert any formula that we come across to 2log(x_opt(i,o)). Here is my complete code:
w1=50rand(24,1);
w2=50rand(24,1);
w=[w1 w2];
K=24; N=2;
cvx_begin
variable x_opt(2,1000);
variable y_opt(2,1000);
for i=1:2
for k=1:K
re2(1+(i-1)U:iU)=pow_pos((x_opt(i,o)-w(k,1)),2)+pow_pos((y_opt(i,o)-w(k,2)),2);
end
end
re=re2’;
[pSolution(:,c)]=getp_convex(re);
for k=1:K
for n=1:N
pkn=sum(pSolution(n,1)); % Pk,n
end
**tempRate(k,1)=log(alpha*(H^2+re(k))+pkn)/log(2);**
end
f=sum(tempRate(:));
Among, tempRate(k,1)=log( alpha*(H^2+re(k))+pkn )/log(2)=log( (alphaH^2+pkn)+alphare(k))/log(2).
(alphaH^2+pkn)=a,
alpha=b,
re(k)=pow_pos((x_opt(i,o)-w(k,1)),2)+pow_pos((y_opt(i,o)-w(k,2)),2).
So, tempRate(k,1)=log( a+ b re(k) ) .
And, I find the reason for the problem is x_opt.^2 and y_opt.^2 in log function.
So, I simplify this as a problem about log(a+b*x opt.^2) .
Thank you for your help.
Presuming b >= 0, then log(a+b*x^2) is convex for b*x^2 <= a and concave for b*x^2 >= a. Therefore it is neither convex nor concave (over the entirety of its natural domain), unless a = 0 or b = 0.