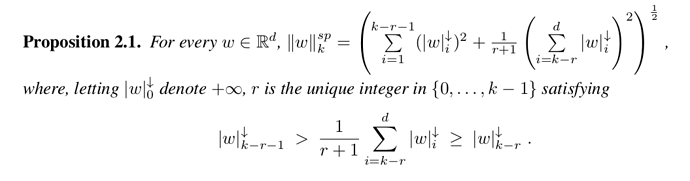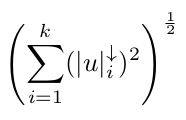I would like to solve a minimization wrt a vector w in R^n of a function F(w) := f(w) + g(w), where f(w) is convex (I can write it in CVX) and g(w) is either (i) the 2-k symmetric gauge function (Bathia - Matrix Analysis 2013) or (ii) the K-support norm (Argyriou, Foygel, Srebro - Sparse prediction with the k-support norm 2012). I am finding difficulties in writing these two norms abiding to the CVX rules. Their definitions are the following:
-
2-k symmetric gauge norm of a vector w in R^n, given a constant k such that 0 < k <= n:
Let u be the vector containing the coordinate-wise absolute values of w.
The 2-k norm of w given constant k is defined as the square root of the sum of the squared k largest components of u.
Since I can upload just one image I will put a formula in the comment below.
-
k-support norm of a vector w in R^n, given a constant k such that 0 < k <= n:
the arrow pointing downwards after a vector means the same vector with elements in descending order.
Any idea? Thanks
2-k support norm formula:
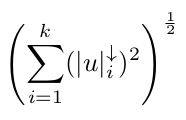
note that “u” here is “w” in the main post, sorry for the confusion.
1 Like
To get you started, the square of the 2-k support norm can be written as sum_largest(square_abs(x),k)
and is convex.
I leave the rest to you (or someone else) as an exercise, ha ha.
1 Like
Thank you for your reply. As sqrt or pow_p with p=0.5 are concave and nondecresing in their argument, they accepts only concave arguments. Is there a way I can take the sqrt of sum_largest(square_abs(w), k) still abiding to the DCP rules?
Another question I have is: in order to compute the k-support norm I need to compute r via for loops and if statements involving my vector w. How can such features be implemented in CVX?
A Matlab code example to compute such norm can be:
function norm_w = ksupp_norm(w, k)
d = length(w);
[beta, ind] = sort(abs(w), 'descend');
temp = sum(beta(k:d));
found = false;
for r=0:k-2
if ( (temp >= (r+1) * beta(k-r)) && (temp < (r+1) * beta(k-r-1)) )
found = true;
break;
else
temp = temp + beta(k-r-1);
end
end
if (~found)
r=k-1;
end
norm_w = sqrt( beta(1:k-r-1)'* beta(1:k-r-1) + temp^2/(r+1) );
end
A free virtual beer to whoever can solve this.
Perhaps someone more capable than me can formulate this as a (computationally intensive) solution to an MIDCP. (I’m not saying it can be done) See http://www.jmlr.org/papers/volume17/15-151/15-151.pdf for some relevant math.
1 Like