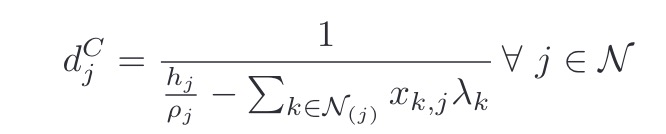
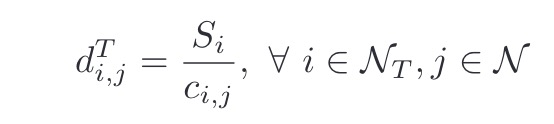
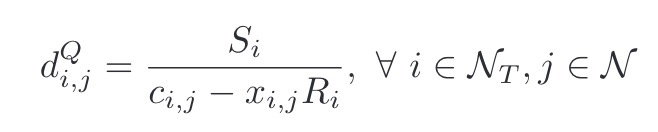

Presuming the denominators are nonnegative, the d terms can be handled with inv_pos,. which automatically imposes nonnegativity constraint on its argument.
There are then product terms between binary and inv_pos Those can be linearized by Big M modeling, presuming you can impose an upper bound on the d terms. I think that can work, even though inv_posis convex and non-affine, because the lower bound inequalities for the lower bound Big M constraints (which would be non-convex) can be omitted due to always being true anyhow. That leaves only the convex Big M constraints. See “Product values” at https://www.fico.com/fico-xpress-optimization/docs/latest/mipform/dhtml/chap2s1.html?scroll=ssecprodval . in which you would treat inv_pos(...) as the continuous variable. You better check to make sure I don’t make a logic error in making this assessment.