Is there any method to solve the sqrt( {convex} ) or {convex} <= {convex} problem

1

I ran into a problem,I need to solve the last constrain in picture1,which the SOCP were used.
1
2
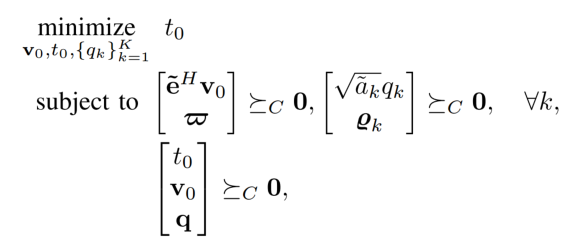
and the constrain actually is
3
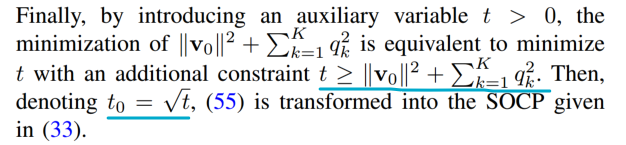
but in CVX, both form is refused, for the reason {convex} <= {convex} and sqrt( {convex} )
4
So I need to express this constrain in what form in CVX?
Thanks!

2

Perhaps the constraint is norm([v0;q]) <= t0

It appears that t does not even appear in the (final version of) the optimization problem. Perhaps sqrt(t) is just something for postprocessing?

But I am guessing because I don;t understand all the notation and conventions in the image you posted. But you undoubtedly would not post a question here unless you intimately understood exactly what the mathematical specification of the optimization problem is, and of course, why it is a convex optimization problem, as you would be aware is your responsibility based on reading the FAQ in an answer to a previous post by you.

Id this is an SOCP, it should be easy to enter in CVX. rotated_lorentz can be used if is a rotated second order cone, although it appears this is not a rotated second order cone.