Is there any form to implement the matrix multiplied by its own conjugate transpose

There is a variable x(2,2) complex
I want to use xx’ in my function.
I only found sum_square_abs(x) to get the diagonal of xx’.
It seems like there is no way to have the full x*x’
Any reformulation to get it out?
Thank you.

Please provide a context for what you want to do. Is your problem actually convex, and if so, how have you determined that? This question will be marked non-convex, unless and until you show you are trying to do something convex.

I don’t have the context with me right now,I will try to prove it later
maybe I could simplify my question.
Can I run it somehow?

cvx_begin
variable x(2,2)
expression y
y=x*x'; %this is not allowed.is that means a matrix multiply its own transpose is an Nonconvex expression?
maximize y
subject to
x(:)<=1
cvx_end

Forget about convexity or DCP rules for the moment. Your program doesn’t make any sense. Your objective function is a 2 by 2 matrix. Your objective function needs to be a real scalar. If you show us what your objective function really is, perhaps further advice can be provided.

Sorry，my mistake.
I will provide my object function next week.

I’m currently facing this problem too, I’m working on my senior thesis on radar signal processing topic. The process appears similar to AXX’A’ (A is a known matrix). I have provided the diagram below to specifically illustrate my problem, where F_BB is the unknown variable in the equation. Is there a specific code to solve XX’, or I need to convert it? Could you give me some advice on this issue?

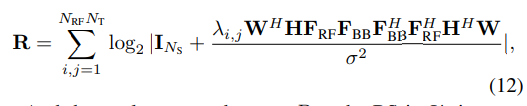
If you defined a new variable (variables?) consisting of F_{BB}F_{BB}^H, which would be declared as hemitian_semidefinite, and presuming \lambda_{i,j} \ge 0, then the argument of log_det would be affine henmitian semidefinite, so R would be the sum of log_det/(...)/log(2) But that would only be viable if F_{BB} is not needed by itself elsewhere in your problem.

Perhaps someone else has a better idea. Is there a determinantal identity which can be used?

But in any event, have you proven your optimization problem is convex?

This is neither convex nor concave in terms of the variable F_{BB}, although it is concave in terms of F_{BB}F_{BB}^H (if \lambda_{i,j} \ge 0).

That is because in the scalar case, log(1+x^2) is convex (in terms of x) for x^2 \le 1, and concave for x^2 \ge 1. Hence it is neither convex nor concave in terms of x.