This happens very often for me. The status is all “failed” but CVX gives me a final result. Is this result reliable for using in papers?
Given the information you provide the answer is maybe.
Have you verified whether the solution make sense to you for instance?
We need more info. for instances log information to say something more precise.
Do the optimization cariables contain anything other than nan ?
This is part of the log for example:
Successive approximation method to be employed.
SeDuMi will be called several times to refine the solution.
Original size: 339 variables, 114 equality constraints
16 exponentials add 128 variables, 80 equality constraints
Cones | Errors |
Mov/Act | Centering Exp cone Poly cone | Status
--------±--------------------------------±--------
8/ 8 | 8.000e+00 9.962e+01 0.000e+00 | Failed
16/ 16 | 8.000e+00 1.867e+01 0.000e+00 | Inaccurate/Solved
8/ 8 | 8.000e+00 2.484e+00 0.000e+00 | Failed
8/ 8 | 8.000e+00s 3.549e-01 0.000e+00 | Inaccurate/Solved
8/ 8 | 8.000e+00s 2.348e-02 0.000e+00 | Failed
0/ 0 | 8.000e+00 0.000e+00 0.000e+00 | Failed
0/ 0 | 8.000e+00 0.000e+00 0.000e+00 | Inaccurate/Solved
0/ 0 | 8.000e+00 0.000e+00 0.000e+00 | Failed
Status: Inaccurate/Solved
Optimal value (cvx_optval): +21.1712
The optimal value makes sense on its own. But when I change the value of some parameters and expect the optimal value to increase it does not work as expected.
The result is not failed. That is the status of an iteration of CVX"s Successive Approximation method. The result is Inaccurate Solved, which might be a valid solution, but not very accurate.
In order to more reliably and accrrately solve the problem:
If you have access to Mosek 9.x, use that with CVX 2.2. II not, follow the directions at CVXQUAD: How to use CVXQUAD's Pade Approximant instead of CVX's unreliable Successive Approximation for GP mode, log, exp, entr, rel_entr, kl_div, log_det, det_rootn, exponential cone. CVXQUAD's Quantum (Matrix) Entropy & Matrix Log related functions .
I see from your posting history that you were aware of CVXQUAD two years ago, so I am a little surprised you were not using it (at least properly) for this problem.
Thanks for your reply Mark. Yes I am aware of the CVXQUAD and have used it many times. It is really more reliable and more accurate. However this time I encountered this error when using it:
unrecognized function or variable ‘op_rel_entr_epi_cone’.
And I could not find much information on the internet how to get rid of this error. So, I went back to the unreliable successive approximation method.
First of all, were you using CVX 2.2? If not do so. Do not use CVXQUAD with CVX 3.0beta.
Second of all, you can try my advice at I am not able to solve this . (except update the advice to use CVX 2.2 rather than CVX 2.1).
If you still encounter an error, and you are using CVX 2.1 or CVX 2.2, perhaps you can provide a complete reproducible problem here or at https://github.com/hfawzi/cvxquad/issues
The most reliable and accurate option is to use CVX 2.2 with Mosek 9.x.
I have the same issue. I see the cvx status as failed with optimal value=NaN but then the result I get seem to be valid as it satisfies all the constraints
@mihirmalladi Please show us the code and the solver and CVX output, as well as evidence that the constraints are all satisfied.
Have you tried specifying a different solver?
I apologize. I have made a comment in this link as well
Here is my cvx function that has to infer a valid Laplacian matrix
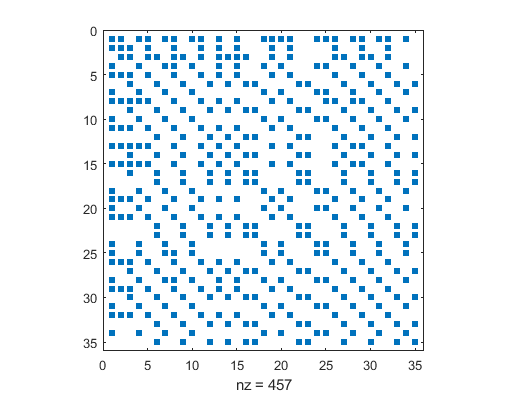
Here is my Laplacian’ spy plot/sparsity
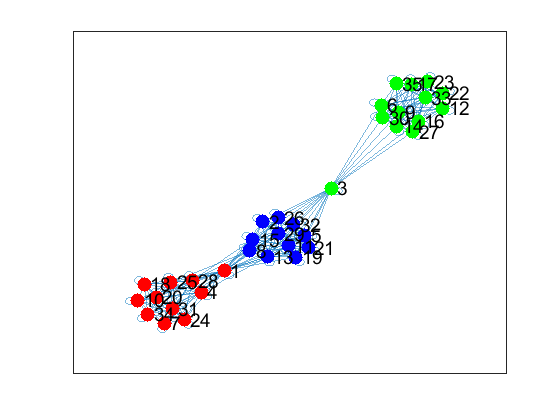
Here is the graph visualization from the inferred Laplacian
The constraints:
- issymmetric(L_D1norm) gives logical 1
- for positive semidefiniteness I am testing on the cholesky factorization
[~,p1]=chol(L_D1norm)
p1 =
0
Hence it looks like it has positive eigen values
3. min(eig(L_D1norm)<0) gives logical 0
4. trace(L_D1norm)=35 which are the number nodes on the graph
5. >> find(vec(L_D1norm-diag(diag(L_D1norm)))>0)
ans =
0×1 empty double column vector
which means that I have non-negative off diagonal entries
The graph visually gives a good partition into three distinct clusters which is what I needed.
This was what it was showing:
Calling SDPT3 4.0: 1898 variables, 631 equality constraints
For improved efficiency, SDPT3 is solving the dual problem.
num. of constraints = 631
dim. of sdp var = 35, num. of sdp blk = 1
dim. of socp var = 637, num. of socp blk = 1
dim. of linear var = 595
dim. of free var = 36 *** convert ublk to lblk
SDPT3: Infeasible path-following algorithms
version predcorr gam expon scale_data
HKM 1 0.000 1 0
it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime
0|0.000|0.000|6.3e+02|1.7e+01|5.2e+06| 1.526493e+00 0.000000e+00| 0:0:00| spchol 1 1
1|0.744|0.169|1.6e+02|1.4e+01|2.8e+06| 7.921068e+03 -8.316494e+01| 0:0:00| chol 1 1
2|0.817|0.858|2.9e+01|2.0e+00|3.8e+05| 8.862879e+03 -3.685697e+02| 0:0:00| chol 1 1
3|1.000|0.948|2.2e-05|1.1e-01|2.5e+04| 5.517002e+03 -2.310728e+02| 0:0:00| chol 1 1
4|1.000|0.581|8.8e-07|4.5e-02|1.2e+04| 2.660357e+03 -2.236909e+02| 0:0:00| chol 1 1
5|1.000|0.472|8.0e-07|2.4e-02|6.5e+03| 2.162006e+03 -2.195472e+02| 0:0:00| chol 1 1
6|0.708|0.933|2.3e-07|1.6e-03|1.5e+03| 1.073481e+03 -2.125223e+02| 0:0:00| chol 1 1
7|1.000|0.573|5.0e-09|7.1e-04|4.9e+02| 2.381452e+02 -2.124065e+02| 0:0:00| chol 1 1
8|0.971|0.603|4.6e-09|2.8e-04|3.5e+01|-1.813088e+02 -2.121119e+02| 0:0:00| chol 1 1
9|0.960|0.973|3.1e-10|8.3e-06|1.3e+00|-2.106488e+02 -2.118963e+02| 0:0:00| chol 1 1
10|0.700|0.743|1.7e-08|2.2e-06|5.4e-01|-2.110665e+02 -2.115876e+02| 0:0:00| chol 1 1
11|0.539|0.389|2.3e-08|1.3e-06|3.9e-01|-2.111280e+02 -2.114977e+02| 0:0:00| chol 2 1
12|1.000|0.167|3.5e-08|1.1e-06|2.8e-01|-2.112250e+02 -2.114725e+02| 0:0:00| chol 2 2
13|1.000|0.403|2.3e-08|6.6e-07|1.8e-01|-2.112686e+02 -2.114078e+02| 0:0:00| chol 2 2
14|0.600|0.325|1.9e-08|4.5e-07|1.4e-01|-2.113531e+02 -2.113777e+02| 0:0:00| chol 2 2
15|1.000|0.131|5.7e-07|3.9e-07|1.8e-01|-2.158019e+02 -2.113689e+02| 0:0:00| chol 5 5
16|1.000|0.015|4.7e-05|3.8e-07|3.0e+01|-1.621997e+04 -2.113685e+02| 0:0:00| chol
linsysolve: Schur complement matrix not positive definite
switch to LU factor. lu 11 30
stop: primal infeas has deteriorated too much, 2.1e+00
17|0.000|0.000|4.7e-05|3.8e-07|3.0e+01|-1.621997e+04 -2.113685e+02| 0:0:00|
number of iterations = 17
primal objective value = -2.11353103e+02
dual objective value = -2.11377667e+02
gap := trace(XZ) = 1.37e-01
relative gap = 3.23e-04
actual relative gap = 5.80e-05
rel. primal infeas (scaled problem) = 1.88e-08
rel. dual " " " = 4.45e-07
rel. primal infeas (unscaled problem) = 0.00e+00
rel. dual " " " = 0.00e+00
norm(X), norm(y), norm(Z) = 9.7e+03, 2.1e+02, 3.0e+02
norm(A), norm(b), norm(C) = 7.6e+01, 2.0e+00, 2.2e+02
Total CPU time (secs) = 0.47
CPU time per iteration = 0.03
termination code = -7
DIMACS: 1.9e-08 0.0e+00 2.7e-06 0.0e+00 5.8e-05 3.2e-04
Status: Failed
Optimal value (cvx_optval): NaN
The primal to dual objective relative gap is not that large, so perhaps SDPT3 (not very accurately) actually solved the problem even though it reported that it ran into numerical difficulties.
Have you tried SeDuMi or Mosek?
It would be less confusing if you kept everything in one thread. There is more relevant info in your post in this thread, so I replied here.
Thank you Dr. Stone @Mark_L_Stone .
This still looks confusing to me.
I tried the same Euclidean Projection optimization on a new data normalized by sigma(=small scalar value). This time cvx has failed to optimize and has not moved to further iterations.
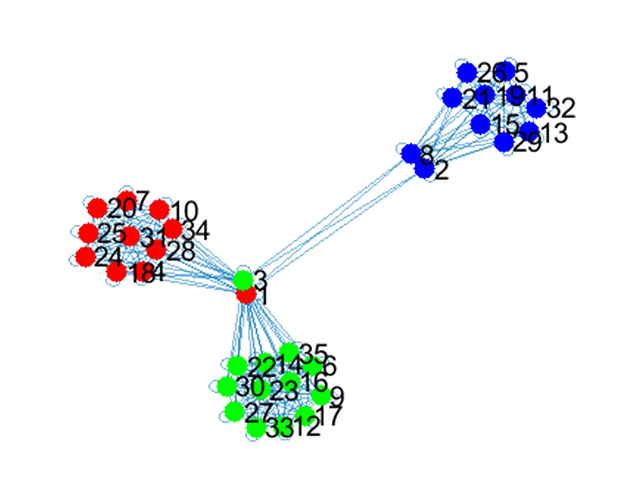
When I commented out the constraint ‘vec(Z-diag(diag(Z)))<=0’ then it was able to solve but it has resulted in giving me the Laplacian matrix with a few positive off-diagonal entries. The resulting graph I got still looks promising in terms of clusters however the Laplacian is not a valid one due to that constraint not being there.
I will take a look at Mosek and SeDuMi.
Have you tired other solvers? Mosek might have the best prospects and provides the best diagnostics, which Mosek employees who post here are expert in interpreting.