Invalid constraint: {convex} >= {convex}

1

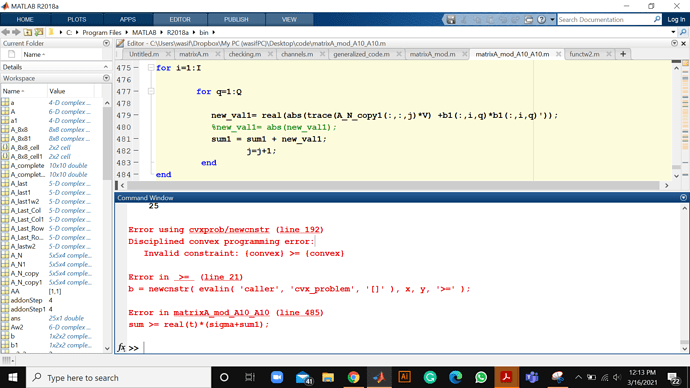
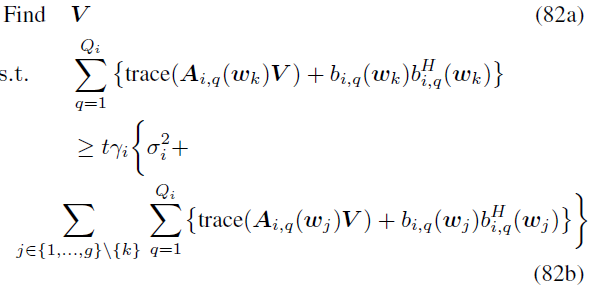I am trying to solve a semidefinite programming problem. Invalid constraint: {convex} >= {convex} , CVX is giving me this error. kindly help me

code is given as:
gamma=1;
sigma=1;
cvx_begin sdp

variable V(1+2Nl,1+2Nl) complex semidefinite
find(real(abs(V)))

subject to
sum=0;
j=1;
for i=1:I

    for q=1:Q
         
       new_val= real(abs(trace(A_N_copy(:,:,j)*V) +b(:,i,q)*b(:,i,q)'));
       
       sum = sum + new_val;
              j=j+1;       
     end

end

sum1=0;
j=1;

for i=1:I

    for q=1:Q
         
       new_val1= real(abs(trace(A_N_copy1(:,:,j)*V) +b1(:,i,q)*b1(:,i,q)'));
       %new_val1= abs(new_val1);
       sum1 = sum1 + new_val1;
              j=j+1;       
     end

end
sum >= real(t)*(sigma+sum1);

for k=1:1+2Nl
real((V(k,k)))<=1;
end
V == semidefinite(1+2Nl);

cvx_end

image

image
image1920×1080 298 KB

2

Are you actually showing the complete CVX program? From what you show, V is the only CVX variable, therefore, the inequality would be {affine >= {affine}

Please show a complete MATLAB session, starting from the beginning of the session until error message occurs.

3

V is initialized as a complex symmetric matrix. for this case, it is a 5*5 matrix

for l = 1:L

phase(:,l)=(2pi)rand(Nl,1);%values in radians
phi(:,:,l) = exp(1i2pi*phase(:,l));
%phi(:,:,l)=diag(d(:,l));
end
phi1=[phi(:,:,1)
phi(:,:,2)];

v = t*[phi1
1] ;

V = v*v’ ;

4

What is this? Readers don’t kmow what the variables are, and you haven’t shown the constraint triggering the error message. Nevertheless, I will guess that v*v' is a disallowed variable multiplication. Are you trying to do a convex relaxation? if so, you should never form v*v'. And if v is not affine, which it does not appear to be, a semidefinite consrraint with it will not be allowed by CVX.

5

sorry for the inconvenience sir, yes I am trying semidefinite relaxation. ‘v’ is initiated as complex, and as I am trying to compute the "trace(A(i,q)V so V=(vv’) to make it symmetric, as you see in the 82(b) equation in the figure posted.

before moving on let make it clear how ‘v’ is initiated

   **for l = 1:L**

**phase(:,l)=(2pi)rand(Nl,1);  %values in radians**
**phi(:,:,l) = exp(1i2pi*phase(:,l)); **
**end %% a vector of (4*1) is generated by using the indexing by using the for loop **

**phi1=[phi(:,:,1); phi(:,:,2)];**

**v = t*[phi1  ; 1]** ; % an axulairy variable is added here which is 't' whose abs =1;

so v=rand(5,1) vector and now for trace computing i have to make it symmtric as mentioned above.

now moving to the CVX portion:
gamma=1;
sigma=1;
gamma=1;
sigma=1;

cvx_begin sdp

variable V(1+2Nl,1+2Nl) complex semidefinite
find(real(abs(V)))

subject to

real(abs(trace(A_N_copy(:,:,1)V) +b(:,1,1)b(:,1,1)')) >= real(t)(sigma(real(abs(trace(A_N_copy(:,:,3)*V) +b(:,2,1)*b(:,2,1)'))

for k=1:1+2*Nl
real((V(k,k)))<=1;
end

V == semidefinite(1+2*Nl);

cvx_end

and at last, I am not being able properly to understand your last comment can you elaborate a bit.

6

disallowed optimization variable multiplication, this mean i have reformulate the problem ?

7

I haven’t looked very carefully at what you’ve done, but fix all of this first. Read Why isn't CVX accepting my model? READ THIS FIRST! .Read the CVX Uers’ Guide. And learn some convex optimization and SDP theory by reading and solving exercises in at least the first 5 chapters of https://web.stanford.edu/~boyd/cvxbook/ .

You can declare V as complex semidefinite, and then not need the ==semidefinite

real(diag(V) <= 1
is simpler and a little faster than using the for loop.

If you are doing a semidefinite relaxation V >= v*v', that should be entered as
[V v;v' 1] == semidefinite(size(V,1)+1)
without ever forming v*v'. The semidefinite constraint is used instead of V = v*v', not in addition to it.

You will need to declare v as a complex vector. if v is the exponential of something else, and that’s what goes in the semidefinite relaxation constraint, that would not be accepted by CVX die to not being affine - but I’m still confused what you’re doing, so I’ll let you straigthen everything out. There may be plenty of other stuff which is wrong and doesn’t make sense.