Invalid computation: geo_mean( {mixed real affine/convex} )

Nonconvex
1

Hi, everyone!
I tried to use CVX to solve a problem with the following constrain in the red rectangle
图片2
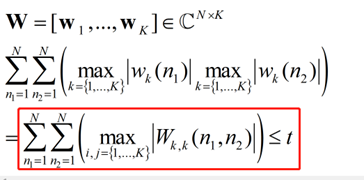
The matrix W is the variable and t is a given constant.
Since the W is the expression of the variable W and is related to multiplication,
I have tried to use the function prod_inv() to formulate the W (i.e, W_hat in the code) in the constrain like this
for n1=1:N
for n2=1:N
w_hat=[abs(W(n1,:)),abs(W(n2,:))];
W_hat(n1,n2)=inv(prod_inv(w_hat));
end
end
The error occurs
image
I have defined the w_hat and W_hat as the expression, and W as complex variable.
What should I do? I would appreciate it if someone could give some advice.

2

I don’t understand the notation, so can’t tell you what to do.

Here is the help for geo_mean.Your argument of ``geo_mean ` clearly violates the rules. have you proven the problem is convex?

help geo_mean

geo_mean Geometric mean.
Y=geo_mean(X), where X is a vector, computes the geometrix mean of X. If any
of the elements of X are negative, then Y=-Inf. Otherwise, it is equivalent
to Y=PROD(X).^(1/LENGTH(X)). All elements must be real.

For matrices, geo_mean(X) is a row vector containing the geometric means of
the columns. For N-D arrays, geo_mean(X) is an array of the geometric means
taken along the first non-singleton dimension of X.

geo_mean(X,DIM) takes the geometric mean along the dimension DIM of X.

geo_mean(X,DIM,W), where W is a vector of nonnegative integers, computes a
weighted geometric mean Y = PROD(X.^W)^(1/SUM(W)). This is more efficient
than replicating the values of X W times. Note that W must be a vector,
even if X is a matrix, and its length must be the same as SIZE(X,DIM).

Disciplined convex programming information:
    geo_mean is concave  and nondecreasing; therefore, when used in CVX
    specifications, its argument must be concave.
3

Hi, Mark! Thanks for your time! Sorry for my bad notation :sweat_smile:
I am not clear about the codes in the cvx funtion prod_inv.m, in which the line 38 is about geo_mean().

In fact, I just want to use the function prod_inv() to formulate the multiplication of two expressions about the varible W. I put the two expressions into a vector w_hat and make sure the elements in the vector w_hat positive by abs(), like this,
w_hat=[max(abs(W(n1,:)));max(abs(W(n2,:)))];

The error occurs in the follow code:
prod_inv(w_hat);

I wonder whether prod_inv() could be used like this, or any other methods would be suggested.

At last, I think my problem might be convex. I have solved it by CVX before I tried to add the additional constraint mentioned above.

Looking forward to your reply!

4

Hi, Mark! Thanks for your time! Sorry for the bad notation :sweat_smile:
I am not clear about the codes in the cvx funtion prod_inv.m, in which the line 38 is about geo_mean().

In fact, I just want to use the function prod_inv() to formulate the multiplication of two expressions about the varible W. I put the two expressions into a vector w_hat and make sure the elements in the vector w_hat positive by abs(), like this,
w_hat=[max(abs(W(n1,:)));max(abs(W(n2,:)))];

The error occurs in the follow code:
prod_inv(w_hat);

I wonder whether prod_inv() could be used like this, or any other methods would be suggested.

At last, I think my problem might be convex. I have solved it by CVX before I tried to add the additional constraint mentioned above.

Looking forward to your reply!

5

You have violated the rules for prod_inv because abs is convex.

Are you sure the problem is convex with this constraint? If it somehow is, it requires reformulation. I will mark it as nonconvex unless proven otherwise.

help prod_inv

prod_inv inverse of the product of a positive vector.
For a real vector, matrix, or X, prod_inv(X) returns 1.0 ./ PROD(X) if
the elements of X are all positive, and +Inf otherwise.

For matrices, prod_inv(X) is a row vector containing the inverse
product of each column of X. For N-D arrays, prod_inv(X) is an array of
inverse products taken along the first non-singleton dimension of X.

prod_inv(X,DIM) takes inverse products along the dimension DIM of X.

prod_inv(X,DIM,P), where P is a positive real constant, computes
prod_inv(X).^P. This is slightly more efficient than the equivalent
POW_POS(prod_inv(X),P).

Disciplined convex programming information:
    prod_inv(X) is convex and nonincreasing in X; therefore, when used
    in CVX specifications, its argument must be concave or affine.

'You wrote “At last, I think my problem might be convex. I have solved it by CVX before I tried to add the additional constraint mentioned above.”

You need to re-read the link I provided.