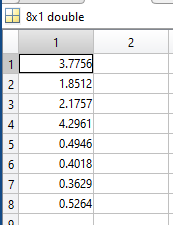
I have an SDP program which is a relaxation of non-convex quadratically constrained quadratic program. Here is my SDP program formulation:
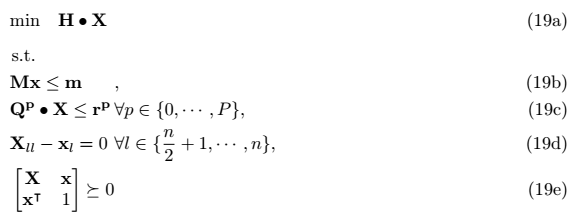
Where n is my number of decision variables (n = 8 in this case), 19b is the LMI for all the linear inequalities, 19c are all the quadratic inequalities (note that there are multiple data matrices Q), 19d to enforce the binary decision variables from n/2 + 1 to n (the second half of the vector x) and 19e to enforce semidefinitness over X (X = xx^T)
Attached the full program with the all the required data matrices:
FULL MATLAB SCRIPT
Here is the output I got from CVX:
Calling SDPT3 4.0: 73 variables, 33 equality constraints
------------------------------------------------------------
num. of constraints = 33
dim. of sdp var = 9, num. of sdp blk = 1
dim. of linear var = 28
*******************************************************************
SDPT3: Infeasible path-following algorithms
*******************************************************************
version predcorr gam expon scale_data
HKM 1 0.000 1 0
it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime
-------------------------------------------------------------------
0|0.000|0.000|7.5e+01|9.9e+00|4.4e+04|-8.082054e+02 0.000000e+00| 0:0:00| chol 1 1
1|0.652|0.844|2.6e+01|1.8e+00|1.5e+04|-6.101845e+02 1.869678e+02| 0:0:00| chol 1 1
2|0.575|0.962|1.1e+01|1.5e-01|7.5e+03|-2.091287e+02 1.032368e+03| 0:0:00| chol 1 1
3|0.167|1.000|9.2e+00|2.5e-02|1.1e+04|-1.798682e+02 2.276281e+04| 0:0:00| chol 1 1
4|0.079|1.000|8.5e+00|7.6e-03|4.9e+04|-1.633760e+02 2.781323e+06| 0:0:00| chol 1 1
5|0.011|1.000|8.4e+00|2.3e-03|2.5e+07|-1.607972e+02 1.903454e+10| 0:0:00| chol 1 1
6|0.011|0.011|8.3e+00|2.3e-03|2.5e+12|-8.344242e+01 1.174126e+14| 0:0:00| chol 1 2
7|0.000|0.000|8.3e+00|2.3e-03|2.5e+12|-2.104616e+02 1.175206e+14| 0:0:00| chol 1 2
8|0.000|0.000|8.3e+00|2.3e-03|2.6e+12|-1.354355e+02 1.180461e+14| 0:0:00| chol 1 2
9|0.000|0.000|8.3e+00|2.4e-03|2.6e+12|-1.403248e+02 1.189495e+14| 0:0:00| chol 1 2
10|0.000|0.000|8.3e+00|2.4e-03|2.6e+12|-1.475756e+02 1.199959e+14| 0:0:00| chol 1 2
11|0.000|0.000|8.3e+00|2.3e-03|2.6e+12|-1.461515e+02 1.211484e+14| 0:0:00| chol 1 2
12|0.000|0.000|8.3e+00|2.3e-03|2.9e+12|-1.447358e+02 1.345997e+14| 0:0:00| chol 1 2
13|0.000|0.000|8.3e+00|2.3e-03|3.9e+12|-1.456245e+02 1.792255e+14| 0:0:00| chol 1 2
14|0.000|0.000|8.3e+00|2.3e-03|5.8e+12|-1.451428e+02 2.708846e+14| 0:0:00| chol 1 2
15|0.000|0.002|8.3e+00|3.5e-03|3.2e+13|-1.452762e+02 1.524154e+15| 0:0:00| chol 1 2
16|0.001|0.000|8.3e+00|3.5e-03|3.9e+13|-1.450579e+02 1.938151e+15| 0:0:00| chol 1 2
17|0.001|0.007|8.3e+00|2.0e-02|7.0e+14|-1.450150e+02 3.587140e+16| 0:0:00| chol 2 3
18|0.001|0.000|8.3e+00|3.9e-02|9.8e+14|-1.447792e+02 5.329337e+16| 0:0:00| chol 2 3
19|0.001|0.036|8.3e+00|4.8e+00|1.1e+17|-1.447188e+02 6.000215e+18| 0:0:00|
sqlp stop: primal problem is suspected of being infeasible
-------------------------------------------------------------------
number of iterations = 19
residual of primal infeasibility
certificate (y,Z) = 5.40e-18
reldist to infeas. <= 4.65e-18
Total CPU time (secs) = 0.10
CPU time per iteration = 0.01
termination code = 1
DIMACS: 1.6e+01 0.0e+00 5.2e+00 0.0e+00 -1.0e+00 1.8e-02
-------------------------------------------------------------------
------------------------------------------------------------
Status: Infeasible
Optimal value (cvx_optval): +Inf
If you have any questions, please let me know in the comments.