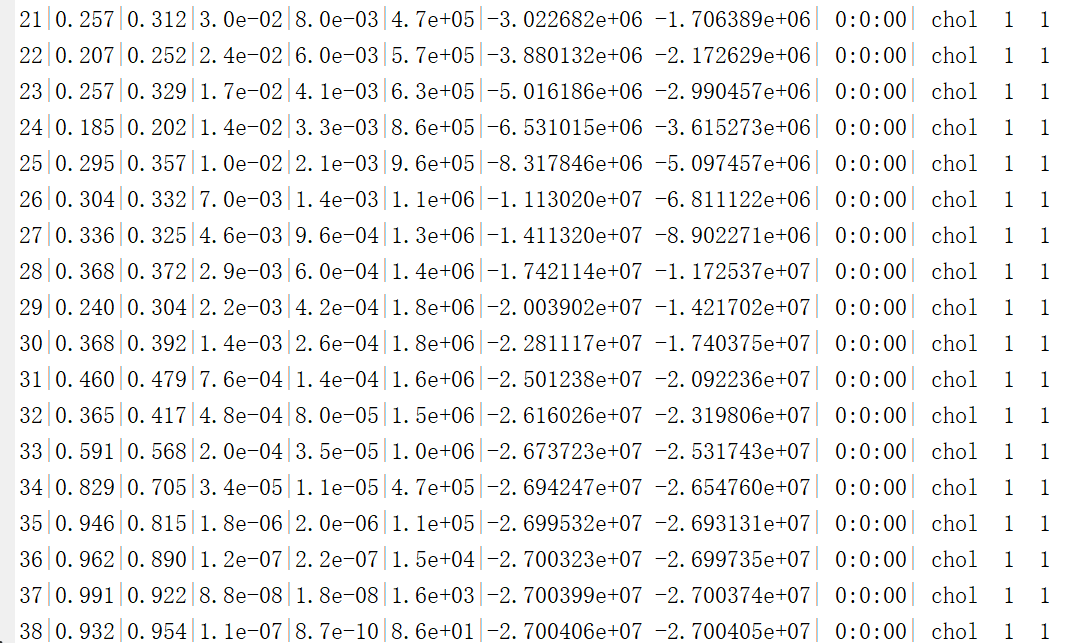
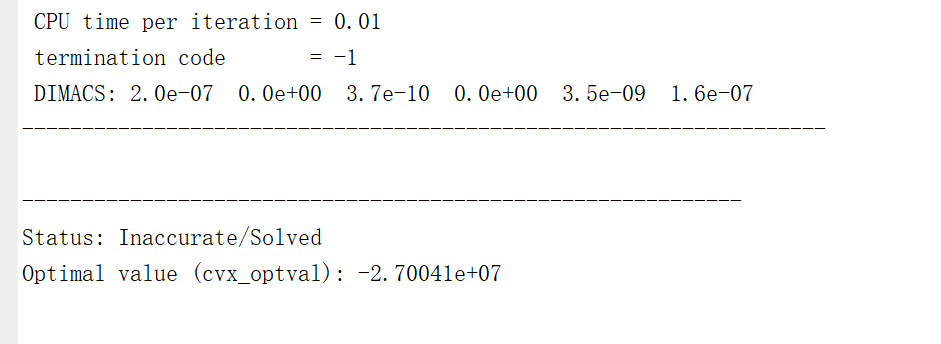the following is my code including two SDPs
the answer of the second SDP is “Inaccurate/Solved”
%%%%%%%%%%%%%% code
clc
clear all
close all
%% 测量点位置
xShip=15*[100;0;-100;-100;-100;0;100;100];
yShip=15*[100;100;100;0;-100;-100;-100;0];
zShip=0; % 发射换能器的入水深度
%% 目标位置
xTar=400randn;
yTar=400randn;
zTar=0;
%% 添加测量误差
detat=10.001; % 时延测量误差
tb=50.001;
c=1500;
cb=5; % 声速测量的固定偏差
detaa=1; % 节点位置的随机误差
xShipMea=xShip+detaarandn(size(xShip));
yShipMea=yShip+detaarandn(size(yShip));
tMea=sqrt((xShip-xTar).^2+(yShip-yTar).^2+(zShip-zTar).^2)/c+detat*randn(size(xShip))+tb;
%% 求解
Qt=detat^2*(ones(length(tMea)-1)+eye(length(tMea)-1));
tdoa=tMea(2:end)-tMea(1);
M=length(tMea);
A=[-ones(M-1,1),eye(M-1)];
G=eye(M-1)-(tdoatdoa’/Qt)/(tdoa’/Qttdoa);
S=[xShipMea’;yShipMea’];
%% 第一阶段 把节点位置当作真值 SDR 估计c0
cvx_begin sdp
variable D1(M,M);
variable d1(M);
variable u(2,1);
variable ys;
minimize(trace(D1A’G’/QtGA));
subject to
[1 d1’;d1 D1]==semidefinite(M+1);
[eye(2) u;u’ ys]==semidefinite(3);
D1(M,M)-ys+2*u’*S(:,M)-S(:,M)‘S(:,M)==0;
for ii=1:M-1
D1(ii,ii)-ys+2u’*S(:,ii)-S(:,ii)'*S(:,ii)==0;
for jj=ii+1:M
D1(ii,jj)-abs(ys-u'*(S(:,ii)+S(:,jj))+S(:,ii)'*S(:,jj))>=0;
end
end
cvx_end
d1e=sqrt((u(1)-S(1,:)‘).^2+(u(2)-S(2,:)’).^2);
c0=(tdoa’/QtAd1e)/(tdoa’/Qt*tdoa);
%% 第二阶段 将节点位置的随机测量误差考虑在内 SDR
Ratio=[10^(-7),10^(-6),10^(-5),10^(-4)];
W=detaa^(-2)*eye(M);
for kk=1:length(Ratio)
cvx_begin sdp
variable d2(M,1);
variable D2(M,M) ;
variable X(2,M+1);
variable Y(M+1,M+1);
minimize 1/c0^2*trace(D2*A'*G'/Qt*G*A)-2*trace(W*X(:,2:M+1)'*S)+trace(W*Y(2:M+1,2:M+1))+Ratio(kk)*trace(D2)
subject to
[1 d2';d2 D2]==semidefinite(M+1);
[eye(2) X;X' Y]==semidefinite(M+3);
for ii=1:M
D2(ii,ii)-Y(1,1)+2*Y(1,ii+1)-Y(ii+1,ii+1)==0;
norm(X(:,1)-X(:,ii+1))-d2(ii) <= 0;
end
for ii=1:M-1
for jj=ii+1:M
D2(ii,jj)-abs(Y(1,1)-Y(1,ii+1)-Y(1,jj+1)+Y(ii+1,jj+1)) >= 0;
end
end
cvx_end
u2(:,kk)=X(:,1);
d2e=sqrt((X(1,1)-S(1,:)').^2+(X(2,1)-S(2,:)').^2);
c2=(tdoa'/Qt*A*d2e)/(tdoa'/Qt*tdoa);
J(kk)=(tdoa*c2-A*d2e)'/Qt*(tdoa*c2-A*d2e);
end
pos=find(J==min(J));
xFinal=u2(1,pos);
yFinal=u2(2,pos);
%%%%%%%%%%%%
the following is the result