Implementing randomized gossip

1

Hi All,
I am trying to implement an this SDP problem (from the paper, Randomized Gossip Algorithms, P. 10 Eq. 54):
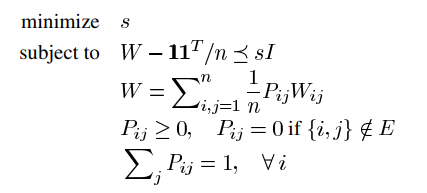
image

My current code is:

cvx_begin 
    variables P(N,N) Wb(N,N) s
    minimize(s);
    subject to
% constraint
    Wb-(one*one')/N<=s*I;
for i=1:N
    q=1:64;
    dif=setdiff(q,i);
    Wb(i,i)==1-(sum(P(i,:))+sum(P(:,i))-2*P(i,i))/(2*N);
    for v=1:length(dif)
    Wb(i,dif(v))==(P(i,dif(v))+P(dif(v),i))/(2*N);
    end
end
for i=1:N
    for j=1:N
        P(i,j)>=0;
    end
end
for i=1:N
    sum(P(i,:))==1;
end
for i=1:N
    nei=neighbors(G,i)';
    % nodes that are not neighbors of node i
    diff=setdiff(nod,nei);
    P(i,diff)==0;
end
cvx_end

There is no error and CVX gives a solution, all the constraints are satisfied as well, but it seems that the solution is not optimal because I find a particular P that leads to a smaller s. I also try to use sdp mode but it doesn’t help.

2

As for your semidefinite constraint, as the constraint is written, if you don’t use sdp mode, the constraint is wrong, because it will be interpreted as elementwise. So either us sdp mode, or rewrite it as s*I - (Wb-(one*one')/N) == semidefnite(N) There might be plenty more wrong with your code, but at least this must be fixed.

This same problem (more or less) has been discussed in How to write the product of CVX variables in a convex way? . I didn’t understand the problem then. and don’t now. But please read that thread.