Implementing a sdp with cvx

1

Hi all,
I’m trying to replicate an author results of a SDP model suggestion using cvx (originally solved with SeDuMi).
The problem to be solved is:
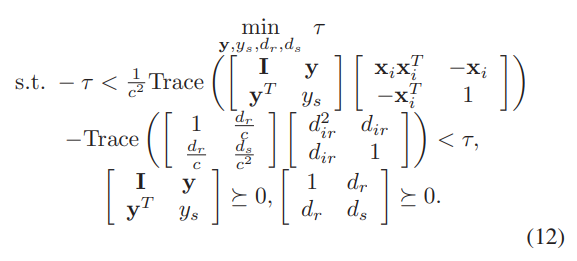
image
where : ys = y’*y, dr = norm(xr-y), ds = dr^2,
In the picture - d_ir, x and xr are all data input.
I wrote this piece of code but struggled with some errors:
the first errors involve the LMI of convex to affine constraints ,
another error with regard to the trace subtraction constraint where {convex} - {convex} is not allowed.

function y = prSDP(x,xr,deltair)
c = 1;
inner_mat = @(y,ys,x) [eye(length(y)),y; y’ ys][xx’,-x; -x’ 1];
inner_mat2 = @(dr,ds,dir) [1 dr/c; dr/c ds/c^2]*[dir^2 dir;dir 1];
inner_mat3 = @(y,ys) [eye(length(y)),y; y’ ys];
inner_mat4 = @(dr,ds) [1 dr ;dr ds];
ds = 0;
cvx_begin sdp
variable y(3,1)
variable tau
dr = norm(xr-y,2);
ds = pow_p(dr,2);
ys = y’*y;
inner_mat3(y,ys) == semidefinite(4,4);
inner_mat4(dr,ds) == semidefinite(4,4);
minimize (tau)
subject to
for ii = 1:length(deltair)
ss1 = sprintf(‘x(:,%d)’,ii);
ss2 = sprintf(‘deltair(%d)’,ii);
eval(sprintf(’ -tau <(0.5/c^2) * trace(inner_mat(y,ys,%s))-trace(inner_mat2(dr,ds,%s))<tau;’,ss1,ss2));
end
cvx_end

I would appreciate any help
Thanks,
Sh.

2

I suggest you study the paper more carefully. You’ve just kind of presented an incompletely described mess. You must follow CVX’s rules. If formulation of a valid CVX program is a mystery, you might email the authors and ask if they can send you code.

3

Hi,
After another careful reading I changed the following constraints:
ys = y’*y, dr = norm(xr-y), ds = dr^2
to the following (with relaxations):
ys >= y’y, dr>= norm(xr-y) , ds == ys -2xr’*y + xr’*xr;
The above did the trick and now it works.

I will appreciate though an explanation for how to tighten these constraints.