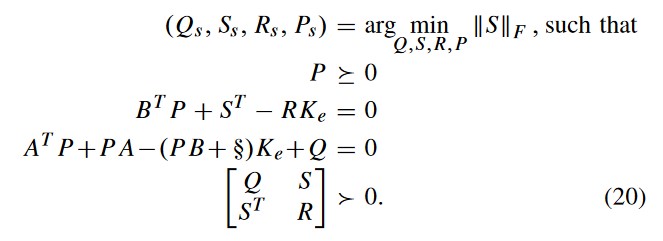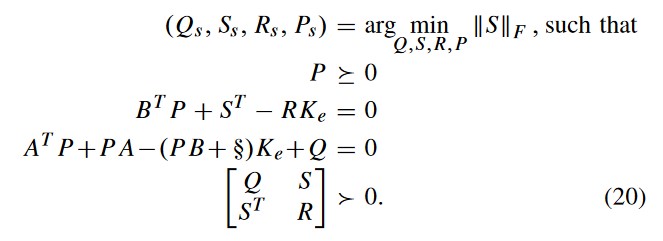
%% Matrix A,B,C
A=[100 0 -1;0 0.1 50;0.333 10 0];
B=[-1 0 10;1 1 0;0.1 -20 4];
C=eye(3);
K=[-3.47 20.2 49.3;3.7 0.0519 0.714;18.7 2.21 4.83];
cvx_begin sdp
variable S
variable P(3,3) symmetric
variable Q(3,3) symmetric
variable R(3,3) symmetric
variable d(3,3) symmetric
minimise(norm(S))
P >= 0;
B’P+S’-RK0== 0;
A’P + PA-(P*B+d)*K+Q==0;
Q > 0 ;
S > 0;
S’> 0;
R >= 0 ;
cvx_end
I need to implement above LMI using cvx, the codes I used are shown above but I am not getting correct final value.
Please help to correct the above
You haven’t implemented the model as shown.
You are missing the LMI: [Q S;S'R] > 0 But actually, CVX treats > as >=. So if you need strict inequality (i.e., positive definiteness), then you’ll need something like
[Q S;S'R] - small_positive_number*eye(6) >= 0 , where small_positive_number is perhaps about 1e-5.
And you will need to declare variable S(3,3), not variable S.
And remove S > 0.
And you can omit Q > 0 and R >= 0
Also, you need minimise(norm(S,'fro')) rather than the 2-norm which is used by default with norm.
I’ll let you check to see whether I missed anything.
%% Matrix A,B,C
A=[100 0 -1;0 0.1 50;0.333 10 0];
B=[-1 0 10;1 1 0;0.1 -20 4];
C=eye(3);
K0=[-3.47 20.2 49.3;3.7 0.0519 0.714;18.7 2.21 4.83];
cvx_begin sdp
variable S(3,3) symmetric
variable P(3,3) symmetric
variable Q(3,3) symmetric
variable R(3,3) symmetric
variable d(3,3) symmetric
minimise(norm(S,‘fro’))
P >= 0;
B’P+S’-RK0== 0;
A’P + PA-(P*B+d)K0+Q==0;
[Q S;S’ R] - 1e-5eye(6) >= 0;
For this result is
Status: Inaccurate/Solved
Optimal value (cvx_optval): +9.02486e-05
Q =
1.9880 1.6727 2.4909
1.6727 4.0435 5.6830
2.4909 5.6830 9.2900
R
R =
0.0110 -0.2243 0.0116
-0.2243 6.5938 -1.3415
0.0116 -1.3415 0.6180
I am trying to implement one example in the paper “Solutions to the Inverse LQR Problem With Application to Biological Systems Analysis”. In this initial value for Q and R are estimated using the above LMI.
Answer given in the paper is
Q=
1.0e+03 *
0.0714 0.0964 0.0628
0.0964 0.3020 0.0086
0.0628 0.0086 1.5500
R=
R =
1.3300 -1.4900 -3.1900
-1.4900 387.0000 -77.0000
-3.1900 -77.0000 53.3000
I don’t believe S should be declared to be symmetric.