I’ve been trying to solve this problem using cvx but I get this error:
Disciplined convex programming error:
Invalid quadratic form(s): not a square.
The given problem is concave in nature. But I’m not sure how to define the function as cvx doesn’t take log functions.
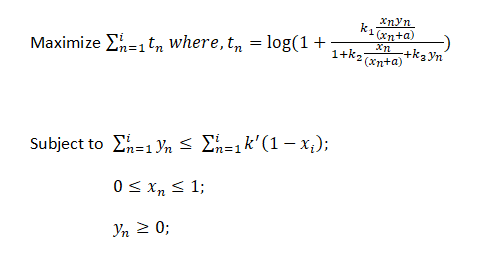
CVX does allow use of log and related functions such as entr and rel_entr. But the arguments of these functions must follow its rules.
Can you show us your proof of concavity?
Concavity does not hold for all parameter and variable values.
For instance, setting n = k1 = k2 = a = 1, the Hessian of the objective function with respect to x and y when evaluated at x = 0.2, y = 0.5 has one positive and one negative eigenvalue; hence the objective function is neither convex nor concave.
Assuming, z= x/x+a which is concave. We prove concavity of log(1+ z*y/(1+z+y)) . The hessian of the function turns out to be non-positive definite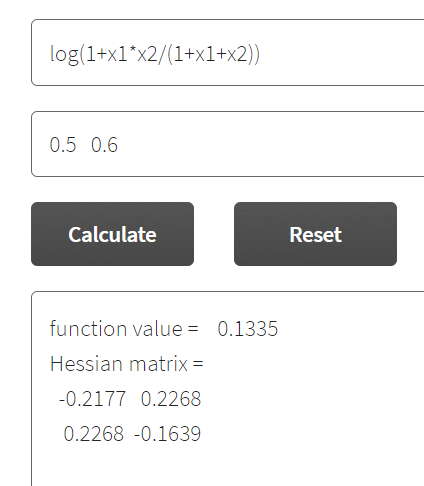 . or if we calculate analytically the Hessian of z*y/1+z+y turns out to be non-positive definite and the function is strictly increasing for z>=0, y>=0
. or if we calculate analytically the Hessian of z*y/1+z+y turns out to be non-positive definite and the function is strictly increasing for z>=0, y>=0
According to my calculations in Maple, the Hessian of log(1+ z*y/(1+z+y)) evaluated at z = 0.2, y = 0.5 has one positive eigenvalue and one negative eigenvalue; hence log(1+ z*y/(1+z+y)) is neither convex nor concave,
The Hessian matrix you show has eigenvalues -0.419 and 0.038, so is indefinite.
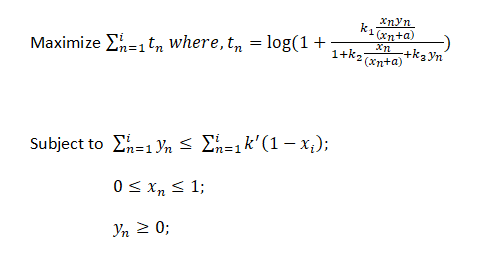
 . or if we calculate analytically the Hessian of z*y/1+z+y turns out to be non-positive definite and the function is strictly increasing for z>=0, y>=0
. or if we calculate analytically the Hessian of z*y/1+z+y turns out to be non-positive definite and the function is strictly increasing for z>=0, y>=0