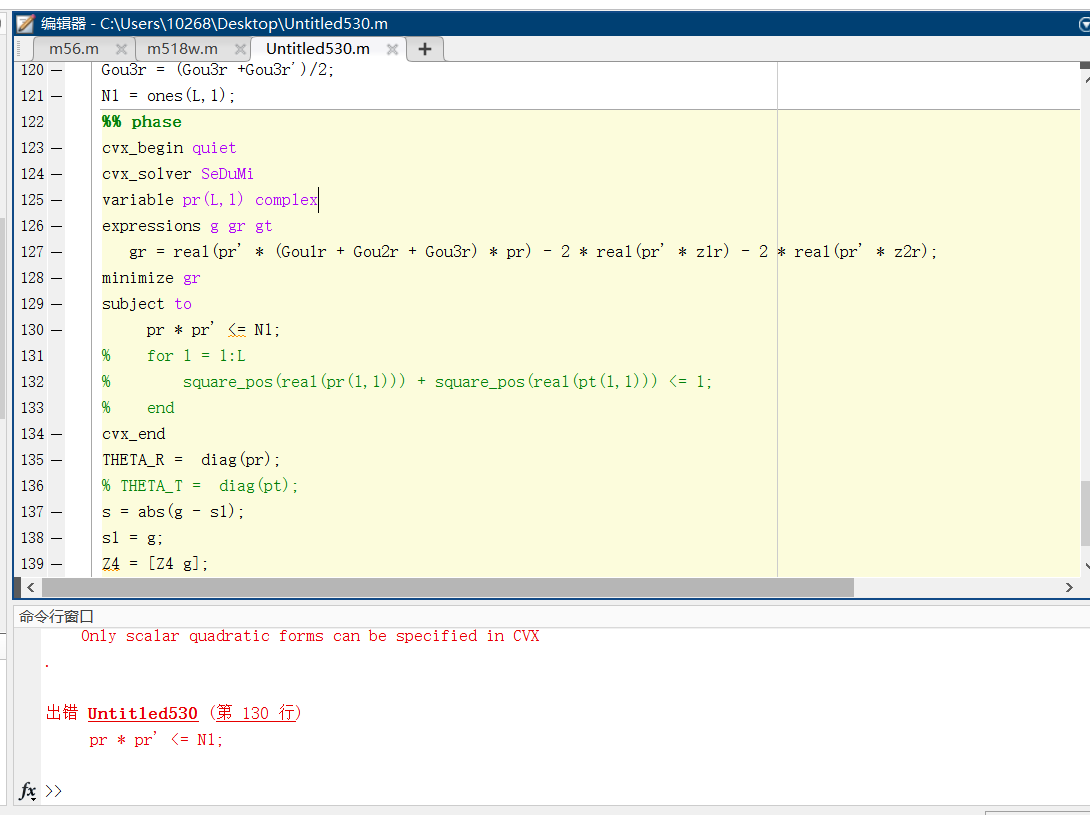
pr*pr' is an outer quadratic form, which is an L by L matrix, whose off-diagonal elements are non-convex, because they are products of (different) variables. Hence the error message.
Do you want pr'*pr <= N ? That is convex and is allowed by CVX. I can’t tell you if that is what you should use, because I don’t know what optimization problem you wish to enter.
No, I actually wanted this pr*pr’ to get every diagonal element of the matrix less than 1, but I never found a suitable expression.
Maybe you want abs(pr) <= N1 ? That constrains the magnitude of every element of pr to be <= N1.
I thought this method does not work. And I change my constraint as this in the figure. I actually wanted this pr*pr’ to get every diagonal element of the matrix less than 1, not the magnitude of every element of pr to be <= N1.
The diagonal elements of pr*pr' are pr(i)*pr(i)'. So if you want those to be <= 1, that would be pr.*pr' <= 1, which is equivalent to abs(pr) <= 1