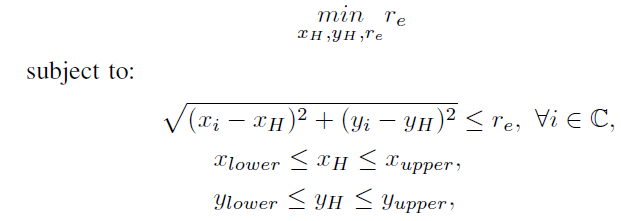I want to ask to solve the socp problem

1

I want to solve this equation.

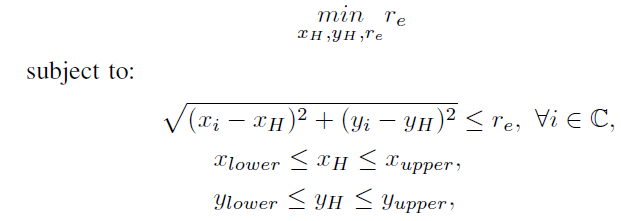
solve

and i make the CVX codes like this.

for i=1:iteration

cvx_begin
variable xh
variable yh
variable re
minimize(re)
subject to
sqrt( (x(i)-xh)^2 +(y(i)-yh)^2 ) <= re
0<=xh<=1
0<=yh<=1

cvx_end

end

but matlab said to me like this.

Disciplined convex programming error:
Invalid operation: sqrt( {positive convex} )

sqrt( (x(t)-xh)^2 +(y(t)-yh)^2 ) <= re

is there anyone who can solve this problem?

Thanks, regards.

2

norm([x(i)-xh; y(i)-yh]) <= re

3

Dear Mark, I’d like to make further inquires about this question. I made some small changes based on the code of ‘orange3644’. Would the two be different?
Thanks!

cvx_begin
variable xh
variable yh
minimize(re)
subject to
for i = 1:iteration
norm([x(i)-xh;y(i)-yh]) <= re
end
0 <= xh <=1
0 <=yh <=1
cvx_end

4

That is a valid way of specifying the norm constraint holds for each value of i from 1 to iteration.

Looking back at the original problem statement, the OP should have placed the for loop inside the cvx_begin ... cvx_end, not outside it. I neglected to point that out. You have done it correctly.