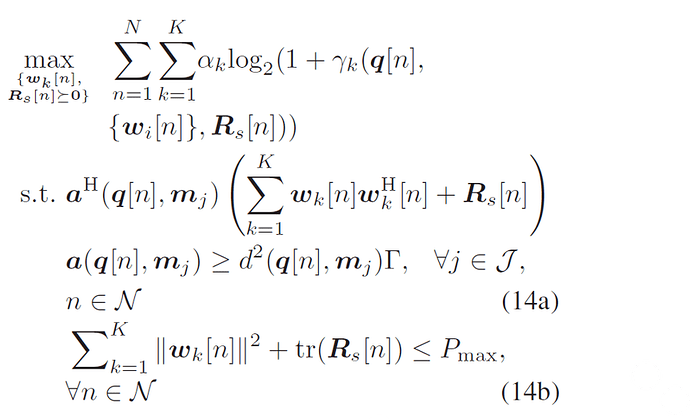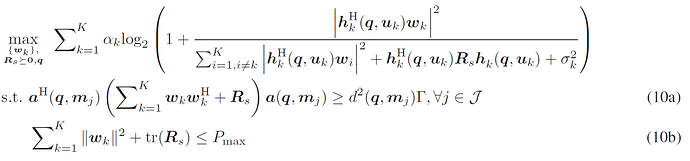I want to solve this problem. a is a steering vector.
In the case of the above problem, since it is decoupled for each time slot, I think it is the same to solve it by dividing it into the following problems for each time slot.
This is the code for the first problem
cvx_begin
cvx_solver Mosek
expressions sum_rate(PARAM.NUM_USER, 1)
expressions objective_1(PARAM.NUM_USER, 1)
expressions objective_1_tmp(PARAM.NUM_USER, 1)
expressions tmp(PARAM.NUM_USER, 1)
expressions tmp_tmp(PARAM.NUM_USER, 1)
expressions objective_2(PARAM.NUM_USER, 1)
expressions objective_2_tmp(PARAM.NUM_USER, 1)
expressions sensing_constraint(PARAM.NUM_TARGET, 1)
variable W(PARAM.NUM_ANTENNA, PARAM.NUM_ANTENNA, PARAM.NUM_USER) complex
variable R(PARAM.NUM_ANTENNA, PARAM.NUM_ANTENNA) complex
for k = 1 : PARAM.NUM_USER
for i = 1:PARAM.NUM_USER
objective_1_tmp(k) = objective_1_tmp(k) + real(trace(channel_t(:,k) * channel_her_t(k,:) * W(:,:,i)));
if i == k
continue;
end
objective_2_tmp(k) = objective_2_tmp(k) + real(trace(B(:,:,k) * (W(:,:,i) - W_t(:,:,i))));
end
tmp(k) = objective_1_tmp(k) + real(trace(channel_t(:,k) * channel_her_t(k,:) * R)) + PARAM.NOISE_POWER_SCALING;
tmp_tmp(k) = -rel_entr(1, tmp(k));
objective_1(k) = tmp_tmp(k) / log(2);
objective_2(k) = alpha(k) + objective_2_tmp(k) + real(trace(B(:,:,k) * (R - R_t)));
sum_rate(k) = objective_1(k) - objective_2(k);
sensing_constraint_tmp = sensing_constraint_tmp + W(:,:,k);
power_constraint_tmp = power_constraint_tmp + real(trace(W(:,:,k)));
end
power_constraint = power_constraint_tmp + real(trace(R));
for j = 1 : PARAM.NUM_TARGET
sensing_constraint(j) = real(steering_target_her_t(j,:) * (sensing_constraint_tmp + R) * steering_target_t(:,j));
end
maximize(sum(sum_rate));
subject to
for k = 1 : PARAM.NUM_USER
W(:,:,k) == hermitian_semidefinite(PARAM.NUM_ANTENNA);
end
R == hermitian_semidefinite(PARAM.NUM_ANTENNA);
power_constraint <= PARAM.P_MAX;
for j = 1 : PARAM.NUM_TARGET
sensing_constraint(j) >= PARAM.SENSING_TH_SCALING * distance_target_t(j)^2;
end
cvx_end
And This is the code for the second problem
cvx_begin
cvx_solver Mosek
expressions sum_rate(PARAM.NUM_USER, PARAM.N)
expressions objective_1(PARAM.NUM_USER, PARAM.N)
expressions objective_1_tmp(PARAM.NUM_USER, PARAM.N)
expressions tmp(PARAM.NUM_USER, PARAM.N)
expressions tmp_tmp(PARAM.NUM_USER, PARAM.N)
expressions objective_2(PARAM.NUM_USER, PARAM.N)
expressions objective_2_tmp(PARAM.NUM_USER, PARAM.N)
expressions sensing_constraint(PARAM.NUM_TARGET, PARAM.N)
variable W(PARAM.NUM_ANTENNA, PARAM.NUM_ANTENNA, PARAM.NUM_USER, PARAM.N) complex
variable R(PARAM.NUM_ANTENNA, PARAM.NUM_ANTENNA, PARAM.N) complex
for n = 1 :PARAM.N
sensing_constraint_tmp = 0;
power_constraint_tmp = 0;
for k = 1 : PARAM.NUM_USER
for i = 1:PARAM.NUM_USER
objective_1_tmp(k,n) = objective_1_tmp(k,n) + real(trace(channel_t(:,k,n) * channel_her_t(k,:,n) * W(:,:,i,n)));
if i == k
continue;
end
objective_2_tmp(k,n) = objective_2_tmp(k,n) + real(trace(B(:,:,k,n) * (W(:,:,i,n) - W_t(:,:,i,n))));
end
tmp(k,n) = objective_1_tmp(k,n) + real(trace(channel_t(:,k,n) * channel_her_t(k,:,n) * R(:,:,n))) + PARAM.NOISE_POWER_SCALING;
tmp_tmp(k,n) = -rel_entr(1, tmp(k,n));
objective_1(k,n) = tmp_tmp(k,n) / log(2);
objective_2(k,n) = alpha(k,n) + objective_2_tmp(k,n) + real(trace(B(:,:,k,n) * (R(:,:,n) - R_t(:,:,n))));
sum_rate(k,n) = objective_1(k,n) - objective_2(k,n);
sensing_constraint_tmp = sensing_constraint_tmp + W(:,:,k,n);
power_constraint_tmp = power_constraint_tmp + real(trace(W(:,:,k,n)));
end
power_constraint = power_constraint_tmp + real(trace(R(:,:,n)));
for j = 1 : PARAM.NUM_TARGET
sensing_constraint(j,n) = real(steering_target_her_t(j,:,n) * (sensing_constraint_tmp + R(:,:,n)) * steering_target_t(:,j,n));
end
subject to
for k = 1 : PARAM.NUM_USER
W(:,:,k,n) == hermitian_semidefinite(PARAM.NUM_ANTENNA);
end
R(:,:,n) == hermitian_semidefinite(PARAM.NUM_ANTENNA);
power_constraint <= PARAM.P_MAX;
for j = 1 : PARAM.NUM_TARGET
sensing_constraint(j,n) >= PARAM.SENSING_TH_SCALING * distance_target_t(j,n)^2;
end
end
maximize(sum(sum(sum_rate)));
cvx_end
The biggest difference was that each variable was added a new dimension with a magnitude of N.
The first problem is that the time slot of the second problem is one, so W and W(:,:,:,1) were compared.
You can see that the values are different as follows
If anyone knows why, please answer.
Thank you for reading!!