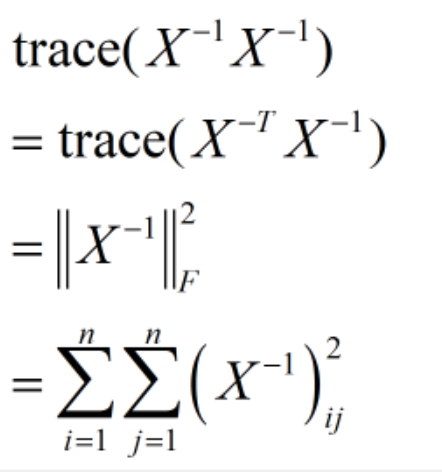How to write trace(inverse(X)*inverse(X)) in the objective function?

Nonconvex
1

My objective function is: min trace(inverse(X)*inverse(X)), where X is a positive definite real symmetric square matrix.

I know that the objective is convex because it can be transformed into a norm form shown below, but I don’t know how to write it in a form that CVX accepts.

I have the derivation:
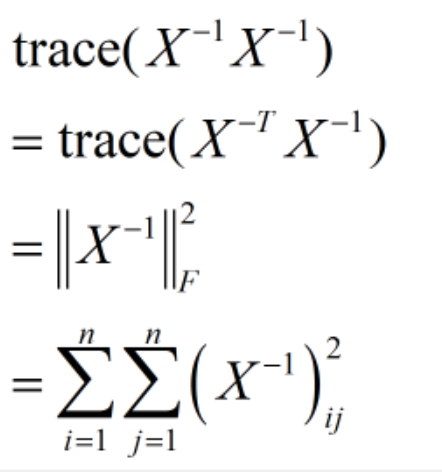
20241021161255

I tried to write the objective function in these forms to let CVX accept:
1) norm form
n = 4; % dimension of the matrix
cvx_begin sdp
variable X(n, n) semidefinite
expression Objtmp
Objtmp = norm(inv_pos(X),‘fro’);
minimize(square(Objtmp))
subject to
X >= 0; % X is PD
cvx_end

CVX error: Disciplined convex programming error:
Cannot perform the operation norm( {convex}, 2 )

2) sum square form
n = 4; % dimension of the matrix
cvx_begin sdp
variable X(n, n) semidefinite
minimize(sum_square(inv_pos(X)))
subject to
X >= 0; % X is PD
cvx_end
However, it gives the error:
Error using cvx/quad_over_lin
The first argument must be affine.

It seems that sum_square() needs sth affine/linear. What we know is that inv_pos(X) is convex.

My questions:

  1. Do you have any suggestions on how to change it here?
  2. inv_pos(X) for matrix X, according to the help, is element-wise, namely 1/x. If I want to have the inverse for the matrix itself. How could I do it?

These questions really bother me a lot. It would be nice if you have some suggestions.

Thanks a lot!
Lu

2

inv_pos is applied element-wise, It is not any kind of matrix inverse.

What you claim to know about it being convex is not true.

However, if X is psd, so is X^2. If you declared a variable X_squared semidefinite, you could use trace_inv(X_squared). But it is not convex in X.

Whether declaration of X_squared rather than X will work for you, depends on whether X is separately needed elsewhere in your problem. Note, writing X >= 0 is redundant (in SDP mode) if X is already declared semidefinite in the variable statement.

3

Thanks for your quick reply.

  1. The reason for saying the objective function (min trace( inverse(X)*inverse(X) )) is convex, is that

  • trace( inverse(X)*inverse(X) ) = norm(inverse(X), ‘fro’ )^2. The norm itself is convex. With the square operation, it is still convex.

  • If X is positive definite, then inverse(X) is also positive definite. It can be proved that inverse(X)*inverse(X) is also positive definite by checking its eigenvalues are all positive. Then, if I minimize a positive definite matrix, the objective is convex.

Or do I misunderstand anything?

  1. I also thought to use a new variable X_squared to replace X*X. But my constraint is a linear function with respect to X, which is A - X > = 0. (A is a known matrix. A-X needs to be positive define.) A-X >= 0 is affine, and therefore convex.

If I define X_squared, the problem becomes

min trace(inverse(X_squared))
s.t. A - sqrt(X_squared) >= 0

However, it seems that sqrt(X_squared) is not linear, so CVX does not accept it for SDP.

It would be really helpful if you could provide some more suggestions about how to handle the original objective *'min (trace( inverse(X)inverse(X) )) or min (norm(inverse(X), ‘fro’ )^2)’ OR the replaced constrain ‘A - sqrt(X_squared) >= 0’.

Thank you very much!

[Please ignore the previous X >= 0, I just did it for a test.]

4

Please re-read the link m ore carefully.Given the extra constraint, your problem appears to be non-convex. norm of an affine expression is convex; but if the expression not affine, it is not generally convex.

You are playing loose with such things as minimizing a positive definite matrix. There is no such thing. You can only minimize a scalar objective function. A positive definite matrix is not a scalar unless it is a 1 by 1 matrix. An objective function created by taking an arbitrary expression of a positive definite matrix is not necessarily positive definite. You can’t use (will not generally be convex) a non-affine expression as argument of a function which would be convex if provided an affine expression as argument.