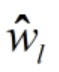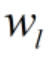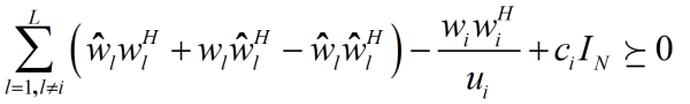How to write this positive semidefinite constraint into CVX?

1

I have this constraint

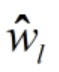
image
image900×136 31.7 KB

where
image
is a N dimensional complex constant column vector,
c_i is a constant and I_N is a N dimensional identity matrix. H at the superscript means conjugate transpose.

Then, the following two are optimization variables
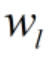
image
is a N dimensional complex column vector.
u_i is a scalar variable

I don’t know how to write this positive semidefinite constraint into CVX

2

if there were only the last two terms on the LHS, then maybe a Scuir complement
[c*eye(N) w’;w u] >= 0 (in sdp mode)

But I’m not sure that can be extended to deal with the terms in the sum, because I think that would invalidate the Schur complement. Maybe someone else knows how to do that.

So your first task is to prove that this is a convex constraint, and specifically, that it can be formulated as a LINEAR SDP