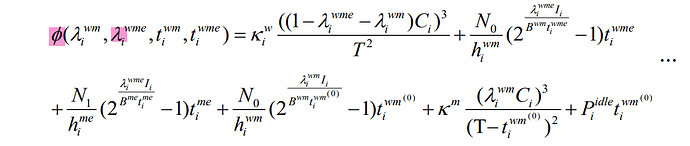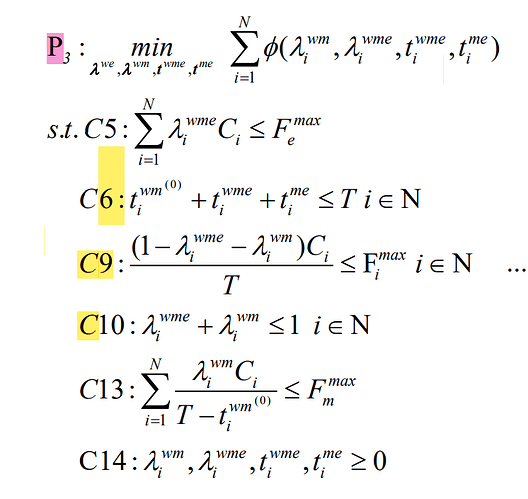Have you proven this is a convex optimization problem,?
The 2 to the (variable divided by a different variable) terms look rather suspect.
This paper I referenced has been shown to be a convex optimization problem, and the main problem I’m facing now is to write several additive formulas into code that conforms to the DCP rules, in particular what is the code for the exponential form of the second additive to write to conform to the DCP rules,thank you so much!
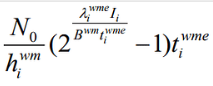
This is what I called into question. Please show us the convexity proof. Before doing so, please re-read, very carefully, the link in my previous post.
Honestly, this paper doesn’t prove that it’s a convex optimization problem either, it just cites other references and then just says it’s obvious. The main thing I want to know now is how this part of the formula code is written to conform to the DCP rules, which has been bugging me for quite some time. Thanks again.
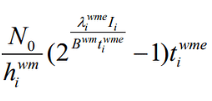
Perhaps you need to re-read the link I posted yet again. I already told you that term looks rather dubious to me.
2^(x/y) is neither convex nor concave if x and y are both variables. If there’s some magic of how the terms combine to result in a convex expressions, it’s not obvious to me. Unless and until a convexity proof is provided, I will declare this problem to be non-convex.
I have no idea what the paper you mention, or the paper it cites, mention. So I make no claim as to their correctness. But as a general matter, I will say that not all statements which are claimed to be obvious are actually correct. And that includes for peer-reviewed papers published in journals.
P4 is NOT what you showed before. P4 is not convex.
w*2^(x/w) is convex and can be handled by exponential cone constraint.
w*2^(x/w) = w*exp(x*log(2)).
So replace w*2^(x/w) with a new variable z, and add the constraint
{x*log(2),w,z} == exponential(1)
You will find that your research, and assistance on your research, will go better if you pay more attention to which claims and mathematical properties go with which formulations. The fact that a paper claims, correctly, that a particular optimization problem in the paper is convex, doesn’t mean that all optimization problems in the paper are convex.