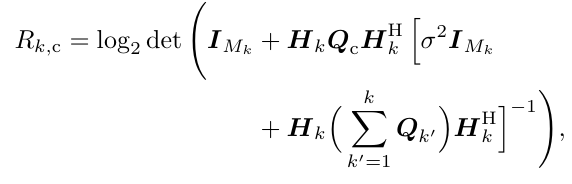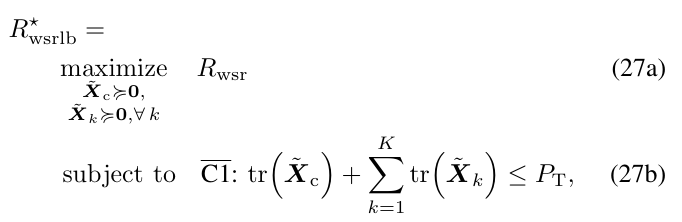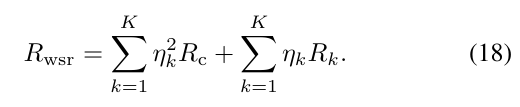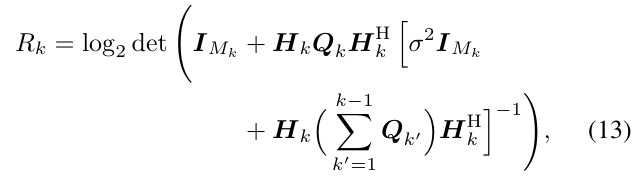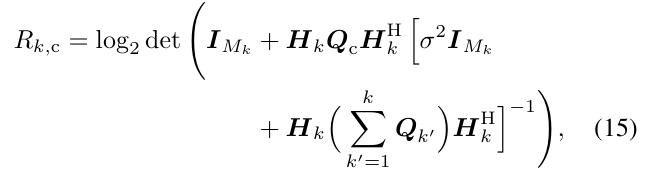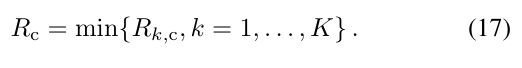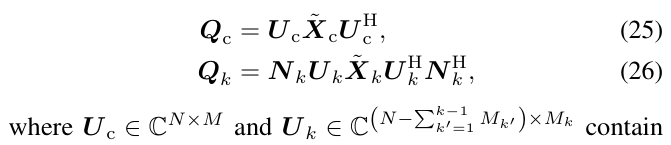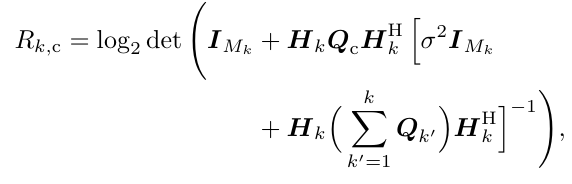
How to write inverse inside the log_det

Nonconvex
1

equation_pic
How to write “inverse term” inside the log2det(eye(2)+some_matrix*inverse term). Above I have attached the equation, where Q_c and Q_k’ are matrix variables with complex values, and remaining other are matrices.
Inside the cvx_begin quiet I am getting following error in MATLAB: Disciplined convex programming
error:
Illegal operation: pow_p(
{complex affine}, {-1} )

Error in cvx/inv_pos (line 5)
y = pow_cvx( x, -1, ‘pow_p’ );

Error in Paper_3_Fig3_Code (line 261)
R_c_1 = log_det(eye(M_1) + H_1*(UcXc_tildUc’)H_1’inv_pos(sigm_sqeye(M_1)+H_1((N_1U1X1_tild*U1’*N_1’))*H_1’))/log(2);

where k=1, Q_c=(UcXc_tildUc’) and Q_1=(N_1U1X1_tild*U1’*N_1’) i.e. Xc_tild and X1_tild are matrix variables here. Please help me how to solve this. Thank you

2

The above equation i.e. error line 261 I have written as follows:
R_c_1 = log_det(eye(M(1)) + H_1*(UcXc_tildUc’)H_1’inv_pos(sigm_sqeye(M(1))+H_1((N_1U1X1_tild*U1’*N_1’))*H_1’))/log(2);

3

Incase if I put inv_pos(real( . )) , then getting error as,

In cvxprob (line 28)
In cvx_begin (line 41)
In Paper_3_Fig3_Code (line 104)
Error using *
Disciplined convex programming error:
Cannot perform the operation
{affine}*{convex}

4

You’re violating CVX’s rules.

To enter this in CVX, the argument of log_det needs to be affine Hermitian definite (PSD). Given the ratio of variables between Qc and Qk, that is not the case. Indeed, Rk,c is neither convex nor concave even in the real scalar case, let alone general complex matrix case. For instance, the special case, log(1+x/(1+y)).

5

Dear sir, in the above equation, need to replace the Qc = UcXc_tildeUc’ , and Qk = NkUkXk_tilde*Uk’*Nk’ , where Xc_tilde & Xk_tilde are optimization variables and are symmetric, positive semi-definite matrices, and others Uc, Uk, Nk are complex valued matrices. I am maximizing rate.

My main question is, how to write inverse here inside that log2det term. I am writing this equation as log_det(eye(2)+some_matrices*inv_pos(.))/log(2) . Is it correct way of writing? or is there any other way (like using norm, etc), Please tell me. Thanks

6

I am defining all variables as,
cvx_begin quiet

% Variables
variable Xc_tild(2, 2) complex
variable X1_tild(2, 2) complex
variable X2_tild(4, 4) complex
variable X3_tild(4, 4) complex

Rkc = log_det(eye(2) + H_1*(Uc*Xc_tilde*Uc')*H_1' *inv_pos(sigma_square*eye(2)*H_1*(N_1*U1*X1_tilde*U1'*N_1')*H_1'))/log(2) ; %for k=1
7

There is no way of entering that expression in CVX.

I told you it is neither convex nor concave even in the real scalar case. So it is neither convex nor concave for complex matrices. Please carefully re-read the link.

8

equation_pic_1
equation_pic_2
equation_pic_3
equation_pic_4
equation_pic_4b
equation_pic_5

Dear Sir, thank you for your patience. Once Please see the above pics (I have attached the full optimization problem that need to solve). Please once see those, and please tell me whether now is it possible to write inside the CVX as I have attached full problem now, If not possible to write, then is there any other suitable tool to solve this? Sorry for disturbing more.

9

It doesn’t look like a convex optimization problem to me, unless there are assumptions and conventions i don’t know about which somehow make it so. Or if somehow the addition of individually non-concave terms winds up being concave.

if the authors claim this is a convex optimization problem, it is up to you to figure out why.

I once again direct your attention to the link I provided.