Read section 4.3.2 “Linear-fractional programming” of http://web.stanford.edu/~boyd/cvxbook/ .
Thank you but can’t i write directly as:
B1=[b0 B]’;
I=eye(3);
cvx_begin quiet
cvx_solver sedumi
variable pow(3,1)
maximize G_0Tpow. * inv_pos(((G_0cTpow)+noise))
subject to
(I-F)*pow>=B1;
pow >= 0;
pow<=Pmax;
cvx_end
That would violate CVX’s rules. Hence, follow the approach in the link I provided.
I solved the problem using CVX by following the given link. Thank you.
Thanks @Mark_L_Stone. I still went ahead and marked this as non-convex because, well, it is. And @Radhika, please read the FAQ to understand why CVX cannot accept the problem as you wrote it.
Using linear transformation i wrote the code:
I=eye(size(F,1));
cvx_begin
cvx_solver
variable W(size(F,1),1)
variable V(1,1)
maximize G_0TW
subject to
(I-F)W-B>=0;
W-Pmax<=0;
W>=0;
G_0cTW+noiseV==1;
V>=0;
cvx_end
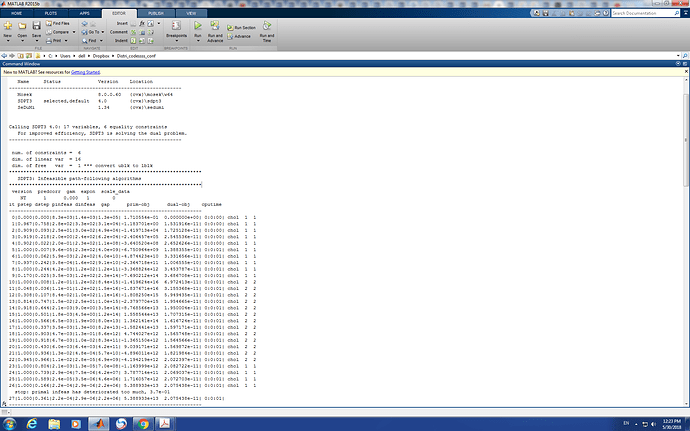
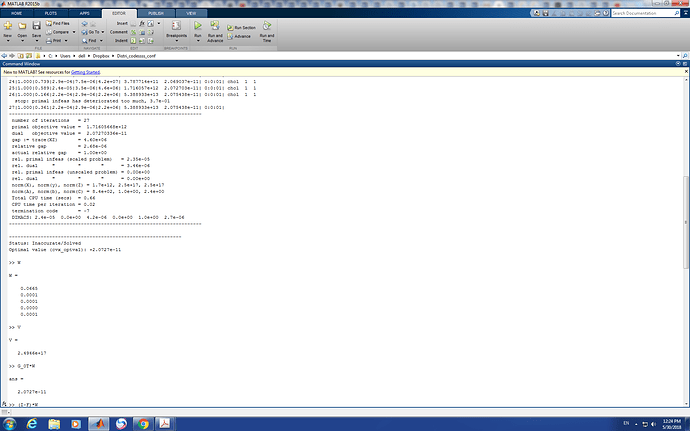
Where F is a square matrix and G_0T is row vector and G_0cT is also a row vector , B is a column vector, Pmax is a column vectoroutput of CVX is:
why this is so?
Hi @Radhika, did you manage to find a fix for your problem?
No sir.
I am seeking for the help.
Why this is coming infeasible or inaccurate.
Dear Sir,
My problem is:
\max \bf\frac{G^T P}{\sigma^2+F^T P}\
\text{subject to:}\
P\geq0\
P\leq P_{max}\
MP\geq \text{K}
here K is a constant number.
This is a quasi convex problem. I am trying to solve its feasibility problem:
\text{find} ~~\bf{P}\\
\text{subject to:}\\
\bf{\frac{G^T P}{\sigma^2+F^T P}}\geq t\\
P\geq0\\
P\leq P_{max}\\
MP\geq \text{K}
My code is:
clc;
clear all;
noise= 10^(((-114) - 30) / 10);
M_LL = 0;
M_UL = 2;
bisec_tol = 1.1;
G=[0 0 0 0
1.20638605033155e-07 0 0 0
0 4.15010746186938e-07 0 0
0 0 6.55662618750864e-08 0
0 0 0 2.54476861575830e-07];
F=[4.13370992652955e-08 1.25251075924258e-13 1.48202098643660e-12 3.07959049028092e-13
0 2.55482980832181e-12 1.25939678651084e-13 3.70693962345198e-12
3.62413277836849e-12 0 5.24777120352613e-14 2.45414843801150e-13
1.62897891862040e-13 3.45987323425213e-12 0 8.96360357556147e-12
3.90330532274798e-13 1.12985845497790e-12 1.68140868778941e-13 0];
PMax=[0.39811;0.12589;0.12589;0.12589;0.12589];
M=[1.0000 -0.6346 -0.0147 -0.0122 -0.0034];
while (M_UL - M_LL >= bisec_tol)
t = round((M_UL+M_LL)./2);
cvx_begin
cvx_solver SeDuMi
variable P(5,1)
subject to
(sum((G.'*P)./(noise+F.'*P))) >= t
P>0;
P<= PMax;
M*P>=3.5306e+11;
cvx_end
if (strcmp(cvx_status,'Solved'))
M_UL = t;
else
M_LL = t;
end
end
Output is:
Error using .* (line 173)
Disciplined convex programming error:
Cannot perform the operation: {real affine} ./ {real affine}
Please tell me what is wrong in this.
(sum((G.'*P)./(noise+F.'*P))) >= t
As the error message says, you are dividing an affine function of the CVX variable P by an affine function of P. That of course is not allowed by CVX.
\frac{G^T P}{\sigma^2+F^T P}
This function is exactly similar to the function mentioned in equation 4.32 of section 4.3.2 of the book entitled “convex optimization” by Boyd. The only difference being is that in my equation I have put_d=0. and this section also tells that the objective function is quasi-convex, so it must be solved by bisection method provided in the section 4.2.5 equation 4.26 and algorithm 4.1. Then why CVX is not allowing to solve this. Doesn’t objective function in equation 4.32 of section 4.3.2 is a division of affine function by affine function"? I am a bit confused. Please sort out my problem.
You can’t enter equation 4.32 directly into CVX. You need to reformulate. Please re-read the book.