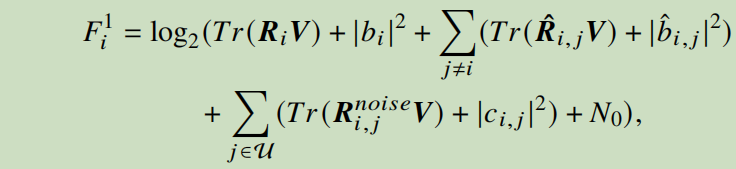The optimization objection is max x, variables are V, x. x is a scalar, V is a matrix, constraint is 0<=x<=F1+F2-F3-F4. Fi is the expression of V, such as the picture
0<=x<=F1+F2 looks like it could be entered “directly” (except use log and divide by log(2)) and would be a convex constraint. But the -F3-F4 is going in the wrong direction for a convex constraint.
oh,thank you .I have used the forst-order Taylor expansion for F3 and F4 , as the picture.But the cvx shows the error for x<=F1+F2-F3-F4: Disciplined convex programming error:
Illegal operation: {concave} - {complex affine} , but F3 and F4 have been expressed as Taylor expansion. I don’t know why ?
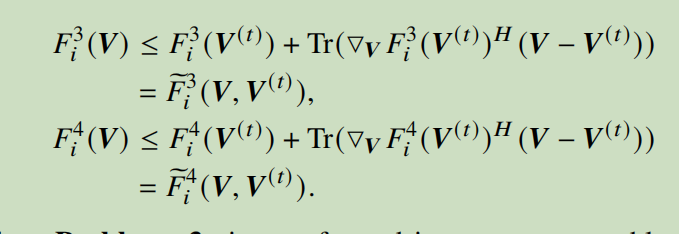
CVX inequalities must be real on both sides.
Are your expressions for F3 and F4 supposed to evaluate to real if there is no roundoff error? If so, just apply real(...) to eliminate the roundoff level imaginary component.
If it is not just roundoiff level imaginary component, real(-F3-F4) would still make this accepted by CVX, but you will have to determine if that is what you want.
Ok ,I will try. Thank you very much! By the way, happy thanksgiving day!