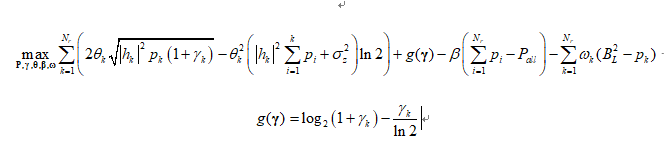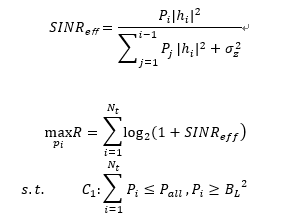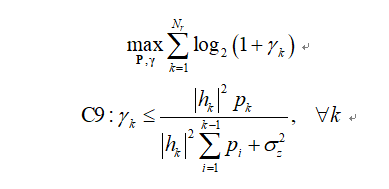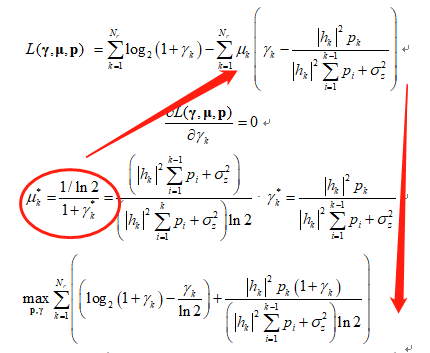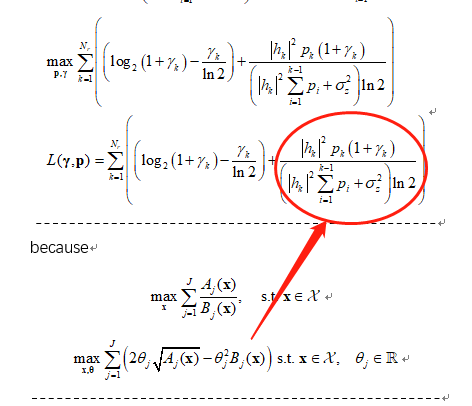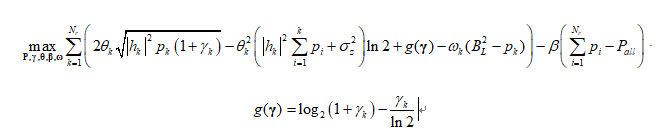How to use CVX in my problem?

1

First I read the paper “Why isn’t CVX accepting my model? READ THIS FIRST!”

So I first transform the nonconvex problem into a convex optimization problem.

    cvx_begin
   H=rand(4,4);Nt=4;Pmax=100;BL=1;
   variable p(Nt) nonnegative;
   variable ganma(Nt) nonnegative;
   variable beta1 nonnegative;
   variable omiga(Nt) nonnegative;
   variable cita(Nt);
   expression R(Nt);
   for i=1:Nt 
       expressions KK(i) WW;
       for j=1:i
          KK(j)=p(j)*(norm(H(:,i)).^2);
       end
%        WW=sum(KK)+1;
      
      R(i)=2*cita(i)*sqrt((norm(H(:,i)).^2)*p(i)*(1+ganma(i)))-cita(i).^2*log(2)*(sum(KK)+1)+(log(1+ganma(i))/log(2)-ganma(i)/log(2));%-beta1*(sum(p)-Pmax)-omiga(i)*(BL^2-p(i));
   end
   maximize(sum(R));
   subject to
     beta1 >= 0;
%      for ii=1:Nt
        ganma >= 0;
        omiga >= 0;
%      end
 cvx_end

Error:
错误使用 .* (line 262)
Disciplined convex programming error:
Invalid quadratic form(s): not a square.

出错 * (line 36)
z = feval( oper, x, y );

出错 text123 (line 39)
R(i)=2cita(i)sqrt((norm(H(:,i)).^2)p(i)(1+ganma(i)))-cita(i).^2log(2)(sum(KK)+1)+(log(1+ganma(i))/log(2)-ganma(i)/log(2));%-beta1*(sum(p)-Pmax)-omiga(i)*(BL^2-p(i));

2

transform Convex problem:
image

4

You are multiplying different CVX variables (expressions), which violates CVX’s rules. Where is your proof that the objective function is concave?

6

1.Original problem:
image

2.then
image

image
3.next
image

4.finally
image

7

THX Mark~~
1Now I use function log() to avoid multiplying different CVX variables. But one of CVX variables-- θ∈R .As we known ,log(x）where x>0.This sub-problem is bothering me now.
2.then I will proof that

8

It is not clear to me exactly what the sub-problem bothering you is. I also don’t understand what the relationships among all the symbols are.

10

1sub-problem: to avoid multiplying different CVX variables,I use function log() to transform multiply(*) into add(+). But the problem is one of CVX variables θ∈R.

Note I show a part of expression
image
this part in matlab is that
log(2cita(i))+0.5(log((norm(H(:,i)).^2)*p(i))+log(1+ganma(i)))

NOW log(2*cita(i)) where cita(i)∈R -> it is bug

11

The question still remains, have you proven this is a convex optimization problem?

Maybe you need to carefully re-read