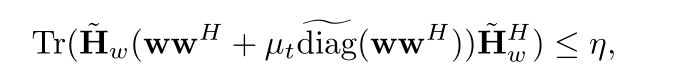Tr(A)<=\eta, where A >=0, \eta is a constant.
What are you trying to do ? This is an affine (linear) scalar constraint (presuming `A is a CVX variable, or is affine in CVX variables).
This can be trivially, but stupidly, reformulated as eta - trace(A) == semidefinite(1), which technically is an LMI if A is affine. I think CVX would just treat is as a scalar inequality
eta - trace(A) >= 0.
Sorry, i may not describe my problem clearly. In fact, i want to transfrom this contraint into a LMI. Where w is a optimization variable, the rest varibales are constant.
This looks familiar: How to use sqrtm function in cvx?
Can you factorize w*w'+mu*diag(diag(w*w')) = factor'*factor, with factor affine in w? If so, it can be reformulated as norm(factor*H','fro') <= sqrt(eta). If not, have you proven it is convex?
BTW, this reformulation, if it can be done, is not an LM, but would be accepted by CVX…
ok, i have got it. thanks