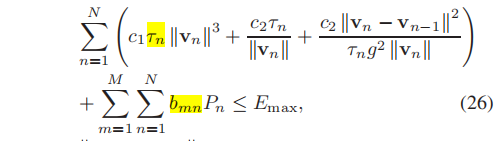Sorry,I din dot express it clearly!
cvx_begin
cvx_quiet(true)
variable un_opt(2,N) nonnegative;
variable bmn_opt(5,N) nonnegative;
variable fmn_opt(5,N);
variable taon_opt(1,N) nonnegative;
variable yita;
maximize yita
subject to
for m = 1:5
for n = 1:N
Imnr(m,n) - Jmnr(m,n)(pow_pos( norms(un_opt(:,n)-GU(:,m)),2) - pow_pos(norms(un0(:,n)- GU(:,m)),2)) >= fmn_opt(m,n); %33
end
end
bmn_opt1 = power((bmn_opt(:,1:N)),2) ;
fmn_opt1 = power((fmn_opt(:,1:n)),2);
sum(sum((bmn0(:,1:N)+fmn0(:,1:N)).(bmn_opt(:,1:N)+fmn_opt(:,1:N))-(1/2).pow_pos(bmn0(:,1:N)+fmn0(:,1:N),2) -(1/2)(bmn_opt1 + fmn_opt1))) >= yita;%34
for i = 1:N
bmn_opt2 = power(bmn_opt(:,i),2);
fmn_opt2 = power(fmn_opt(:,i),2);
sum((bmn0(:,i)+fmn0(:,i)).*(bmn_opt(:,i)+fmn_opt(:,i))-(1/2).*power(bmn0(:,i)+fmn0(:,i),2) -(1/2).*(bmn_opt2 + fmn_opt2)) >= Rmin .*taon_opt(1,i);%35
end
vn = rand(1,N);
v0 = 15;
for i_ = 1:N
sum(bmn_opt(:,i_)) <= taon_opt(1,i_); %15
end
for i = 2:N
norms(un_opt(:,i)- un_opt(:,i-1)) <= samax;% 约束21
un_opt(:,i) - un_opt(:,i-1) == ((vn(1,i) + vn(1,i-1))./2).taon_opt(1,i); %23
norms(taon_opt(1,i)) <= abs((vn(1,i) - vn(1,i-1))./amax); %27
end
norms(un_opt(:,1) - ui(1,1)) <= samax;
un_opt(:,1) - ui(1,1)== taon_opt(1,1)(vn(1,1) + v0)/2;
norms(taon_opt(1,1)) <= abs((vn(1,1) - v0(1,1))./amax);
for i = 1:5
for i_ = 1:N
bmn_opt(i,i_) >= 0;
end
end
aa1 = 0;
for i = 2:N
aa3 = (c1.*taon_opt(1,i).*pow_pos(vn(1,i),3) + c2.*taon_opt(1,i)./norms(vn(1,i)) + (c2.pow_pos(norms(vn(1,i) - vn(1,i-1)),2))./((inv_pos(taon_opt(1,2:N)+eps).(g^2).*vn(1,2:N))));
aa1 = aa1+aa3;
end
aa1 = aa1 + (c1.*taon_opt(1,1).pow_pos(vn(1,1),3) + c2.taon_opt(1,1)./norms(vn(1,1)) + (c2pow_pos(norms(vn(1,1) - v0),2))./((inv_pos(taon_opt(1,1)+eps).(g^2).*vn(1,1))));
aa2 = sum(sum(bmn_opt(:,1:N).*Pn(1,N)));
aa1 + aa2 <= Emax; %26
cvx_end
val1= cvx_optval;
un0 = un_opt;
bmn0 = bmn_opt;
fmn0 = fmn_opt;
taon = taon_opt;