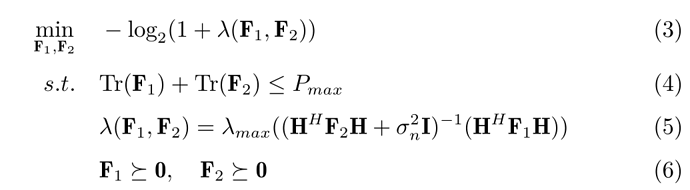Apparently you did not understand when I said not to start multiple threads with the same topic. Did you study the link Previously provided?
sorry,i have read the book roughly,but i don’t know how to solve this problem using cvx, can you help me? i think my problem is very difficult, i really don not know how to solve this problem.
If you studied that book for that short a time and don’t understand convex formulation of generalized eigenvalue problem, you didn’t study it hard or long enough. This forum is not a crutch for you to avoid intellectual effort.
ok thank you i will read the book again, thank you very much.
Did you CAREFULLY study section 2.2.3 “Generalized eigenvalue problems” of https://web.stanford.edu/~boyd/lmibook/lmibook.pdf , and then the bisection method described in section 4.2.5 “Quasiconvex optimization” of Boyd and Vandenberghe “Convex Optimization” . This may take you some time, especially, if you have to study preceding material in order to understand those sections.
thank you. i learn these section carefully now. thank you very much
indent preformatted text by 4 spaces
clc,
clear;
close all;
epsilon = 1e-3;
low_bod = -200;
upper_bod = 200;
iter_num = 100;
Nt = 10;
Ne = 4;
sigma = 1;
H = rand(Nt,Ne);
Pmax = 1;
t = 100;
for iter = 1:100
t = (low_bod+ upper_bod)/2;
cvx_begin sdp quiet
variable F1(Nt,Nt) hermitian semidefinite
variable F2(Nt,Nt) hermitian semidefinite
subject to
lamda_max((H'*F2*H+sigma^2*eye(Ne))\(H'*F1*H)) -t<=0
% subject to
% real( trace(F1))<=Pmax
real(trace(F1) + trace(F2))<=Pmax
cvx_end
if strcmp(cvx_status,'Solved')
upper_bod = t;
else
low_bod = t;
end
if abs(upper_bod-low_bod)<=epsilon
break;
end
disp(iter)
end
e=eig((H'*F2*H+sigma^2*eye(Ne))\(H'*F1*H));
min(e)
hello i want to use bisection algorithm to solve the generalized eigenvalue problem(quasi-convex optimization),but i meet a error in using lamda_max function, can you help me?
First of all, is your original problem a Generalized eigenvalue programming? Can you tell us why?
yes, my original problem a Generalized eigenvalue programming, lambda_max(A,B) is a quasi-convex function, which can be solved by bisection method, so i want to use bisection algorithm to solve this problem
indent preformatted text by 4 spaces
clc,
clear;
close all;
epsilon = 1e-3;
low_bod = -200;
upper_bod = 200;
iter_num = 100;
Nt = 10;
Ne = 4;
sigma = 1;
H = rand(Nt,Ne);
Pmax = 1;
t = 100;
lambda0 = 100;
val = zeros(iter_num,1);
for iter = 1:100
cvx_begin quiet
variable F1(Nt,Nt) hermitian semidefinite
variable F2(Nt,Nt) hermitian semidefinite
subject to
lambda0*(H'*F2*H+sigma^2*eye(Ne))- (H'*F1*H)==semidefinite(Ne)
(H'*F2*H+sigma^2*eye(Ne)) ==semidefinite(Ne)
real(trace(F1) + trace(F2))<=Pmax
cvx_end
cvx_begin sdp quiet
variable lambda
minimize (lambda)
subject to
lambda*(H'*F2*H+sigma^2*eye(Ne))- (H'*F1*H)==semidefinite(Ne)
cvx_end
lambda0 = lambda;
val(iter) = lambda;
disp(iter)
end
e=eig((H'*F2*H+sigma^2*eye(Ne))\(H'*F1*H));
min(e)
i
How did(23) become (27)?
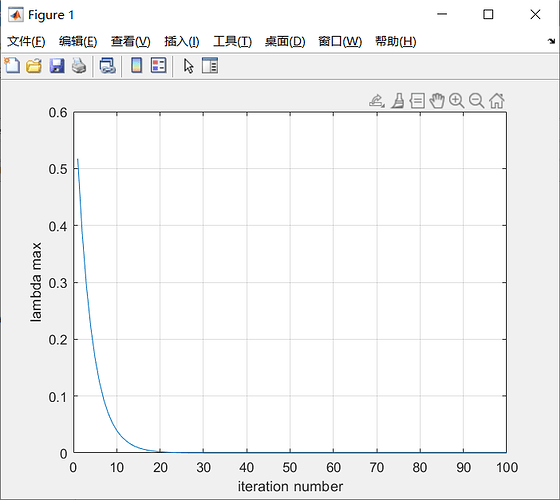
23->27 is based on the figure, i want to alternatively optimize {F1,F2} and lambda to miminize lambda_max,the convergence curve is shown in the second figure,
i not sure this processing is right or not, can you help me?
23->27 is based on the figure, i want to alternatively optimize {F1,F2} and lambda to miminize lambda_max,the convergence curve is shown in the second figure,
i not sure this processing is right or not, can you help me?
I don’t know much about this really.
hello, i have soved the generalized eigenvalue problem based on alternative optimization, but i am not sure the optimization proceeding is right or not, can you help me? thank you