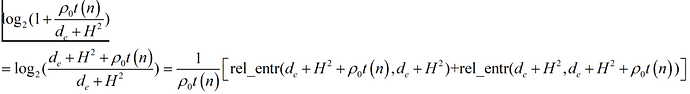How to solve the problem?

This is the code that reports the error:
tempee(n) =log(2) * (1 / tempt(n) * rho) * (rel_entr_quad(tempt(k , n) * rho + H^2 , d_e +H^2) + rel_entr_quad(d_e +H^2 , tempt(k , n) * rho + H^2));
The readers of the forum can’t know what this is. We don’t know what are CVX variables, CVX expressions, or input data.
I apologize for not expressing what I wanted to say clearly.What I want to express is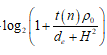 In the formula, the variable is de, but in cvx directly write this formula, there will be log(convex) this error, I will convert the formula into “rel_entr” function,but after this conversion, run cvx will appear Cannot perform the operation: {positive constant} .* {convex}. I tried breakpoint analysis in matlab and found that the error occurs because t(n) = 0,I tried breakpoint analysis in matlab and found that the error occurs because t(n) = 0,But in fact, I need t(n) = 0.How do I go about solving it?
In the formula, the variable is de, but in cvx directly write this formula, there will be log(convex) this error, I will convert the formula into “rel_entr” function,but after this conversion, run cvx will appear Cannot perform the operation: {positive constant} .* {convex}. I tried breakpoint analysis in matlab and found that the error occurs because t(n) = 0,I tried breakpoint analysis in matlab and found that the error occurs because t(n) = 0,But in fact, I need t(n) = 0.How do I go about solving it?
This is the mathematical conversion process:
if t(n) = 0, the expression evaluates to zero.
If t*n)*rho >= 0 and d_e >= 0, I believe the expression is convex, and I suspect is representable in CVX, but I will leave it to someone else to confirm and derive the representation.
Thanks for your help! But now the problem is that running the code in cvx for the above case gives cvx an error when t(n)=0: Cannot perform the operation: {positive constant} . * {convex}. So, how do I solve this problem?
O.k., I see now that you actually do have a CVX-representable formula for your desired expression, although you need to divide by log(2).
As for t(n)=0, t(n) is input data. As I wrote earlier, the (original) expression evaluates to zero when t(n) = 0. So treat it accordingly in your program, i.e., use zero rather than the rel_entr formula when t(n) = 0. Such conditional is allowed because it is conditional on input data, not on a CVX variable or expression.
Note: I should have recognized that your formula is the already known formula at Writing x*log(1+x/y) , with both sides divided by x, which works as long as x is a non-zero constant.