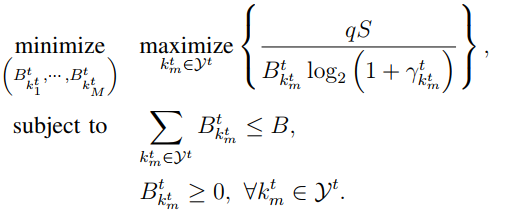
where ![]()
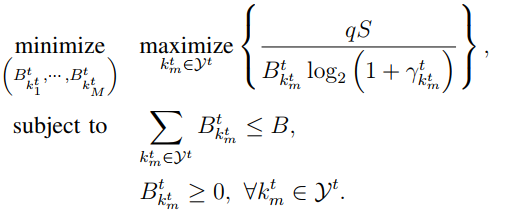
where ![]()
Presuming \gamma, q, and S are all > 0 it looks something like
variable B(n)
minimize(max(inv_pos(B.*log(1+GAMMA))))
where I haven’t bothered with positive constant multiplicative factors in the numerator, and GAMMA is the vector of \gamma values.
I’ll let you modify this code to handle whatever messier indexing notation is actually used in your problem.
On the other hand, if there are hidden variables lurking somewhere (if q, S or the GAMMA vector are not constants), this may not work,.
Thank you very much, Mark. However, for this question, what I understand is to minimize the largest term, but how to understand ‘maximize’ ? How can I find the largest term?
That’s what my code does, based on my guess as to what the notation means.
Given
min z
st. y_i <= z, for all i
it is easy to see that the optimal z will be equal to maximum of y.
@Erling has shown you what CVX does with the max in my code. You can use his construct or max. Take your choice.
Many thanks for your reply, it is inspired me a lot.
Thanks a lot. And it is so kind of you both. I will try to solve the problem using the methods provided by both of you.